11449 Find the maximum and minimum values of f=(a3+b3+c3)2/((a2+b2)(a2+c2)(b2+c2)) given that a,b,c are positive and a+b≥c and a+c≥b and b+c≥a.
Solution:
The domain of f is the part of the open first octant of a,b,c-space that is inside the infinite tetrahedron with faces a+b=c, a+c=b, b+c=a.
Now f is constant on each open straight half line that starts from (0,0,0) and stays in the domain.
So we only have to consider values in a+b+c=1 with a∈(0,1/2], b∈(0,1/2], a+b∈[1/2,1).
I did this with Maple and found the global minimum 9/8 for a=b=c and the global maximum 2 for a=b=c/2 or a=c=b/2 or b=c=a/2.
First I had the range [9/8,2) in mind, considering (a,b,c)=(t,t,t) and (a,b,c)=(0,t,t) etcetera. Here (0,t,t) is not in the domain.
But then, much to my surprise, I discovered the value 2 for a=b=c/2 (etcetera).
(I suppose the proposer of the problem doesn't ask for nonglobal extreme values.)
11455 Determine the triangles T of maximal area in the Cartesian plane with the property that for all nonzero integer pairs (m,n) the interiors of T and T+(m,n) are disjoint.
Partial solution:
I think I found a triangle T with a large area among the ones that meet the conditions, although I don't know whether T is optimal.
It's the equilateral triangle with vertices (0,0) and (ρ,ρ) with sides going through (1,0) and (ρ,ρ-1).
Then ρ=tan(75)/(1+tan(75)), where tan(75)=√((1/2+(1/4)*√3)/(1/2-(1/4)*√3)).
So the area of T is (1/4)*√3*2*(tan(75)/(1+tan(75)))2.
This is about 0.538675..
Solution:
I first ran a simulation program:
program frog;
var t,k,m,n:integer; a:array[0..30000,0..30000] of integer;
begin
while true do begin
writeln('n?'); readln(n);
for t:=0 to 30000 do for k:=0 to n do a[t,k]:=0;
for m:=1 to 30000 do
begin
k:=0; a[0,0]:=a[0,0]+1;
for t:=1 to 30000 do
begin
if not random≥1-k/n then k:=k-1 else k:=k+1;
a[t,k]:=a[t,k]+1
end
end;
for k:=0 to n do
writeln('limprobodd[',k:3,'] = ', (a[29999,k]/30000):13:10, ' limprobeven[',k:3,'] = ',(a[30000,k]/30000):13:10);
writeln; readln; writeln end
end.
I studied the output and noticed:
1) After an even number of hops, the frog is in a box with an even number, and after an odd number of hops in a box with an odd number, so
lim p2t(k) = 0 iff k is odd and lim p2t+1(k) = 0 iff k is even.
2) For each n the table of limits (p2t+1(k),p2t(k)) is symmetric, because the probability of a hop to the right at the left side is equal to the probability of a hop to the left at
the right side.
For instance, for n=3 we have (0,1/4),(3/4,0),(0,3/4),(1/4,0) and for n=4 (0,1/8),(1/2,0),(0,3/4),(1/2,0),(0,1/8)
Then I found an exacter way to approximate the numerical values of the nonzero limits:
program frog2;
var k,n,t:integer; p:array[0..100,0..30000] of real;
begin
while true do begin
writeln('n?'); readln(n);
for k:=0 to 100 do p[k,0]:=0;
p[0,0]:=1;
for t:=1 to 30000 do
begin
for k:=1 to n-1 do p[k,t]:=(1-(k-1)/n)*p[k-1,t-1]+((k+1)/n)*p[k+1,t-1]
end;
for k:=0 to n do writeln(p[k,29999]:13:10,'*',p[k,30000]:13:10);
writeln; end
end.
Now I thought I had to sum over all possible paths to box k to find the exact values.
But, thinking it over, I found I only had to solve a system of linear equations (for k=0,1,...,n):
(For odd k let pk:=lim p2t+1(k) and for even k let pk:=lim p2t(k).)
(For convenience, let p-1 = pn+1 := 0.)
pk = pn-k,
pk = (1-(k-1)/n)*pk-1 + ((k+1)/n)*pk+1
SUM(k even: pk) = 1 = SUM(k odd: pk)
I noticed that we can solve this system of linear equations for any fixed n.
For instance, I found for n=4 for the eventime limits (1/8,0,3/4,0,1/8) and for the oddtime limits (0,1/2,0,1/2,0), as I did earlier above.
For n=5 I found for the eventime limits (1/16,0,5/8,0,5/16,0) and for the oddtime limits (0,5/16,0,5/8,0,1/16).
Now I still had to find the solution for the general case.
Working from k=1 to greater k, I soon discovered pk = (n over k)*p0.
Then, using SUM(k even: pk) = 1 = SUM(k odd: pk), I finally found pk = (n over k)*21-n.
11500 We have n balls, labeled 1 through n, and n urns, also labeled 1 through n. Ball 1 is put into a randomly chosen urn. Thereafter, as j increments from 2 to n, ball j is put into urn j if that urn is empty, otherwise, it is put into a randomly chosen empty urn. Let the random variable X be the number of balls that end up in the urn bearing their own number. Show that the expected value of X is n - Hn-1.
Solution:
First I ran the following program:
program urns;
var j,n,keuze,aantal:0..10; som,t,x:real; klaar:boolean; urn:array[1..10] of 0..10;
begin
som:=0; t:=0; writeln; writeln('n?'); readln(n);
while true do
begin
t:=t+1;
for j:=1 to n do urn[j]:=0;
keuze:=random(n)+1;
urn[keuze]:=1;
for j:=2 to n do
if urn[j]=0 then urn[j]:=j
else
begin
klaar:=false;
repeat
keuze:=random(n)+1;
if urn[keuze]=0 then begin urn[keuze]:=j; klaar:=true end
until klaar=true
end;
aantal:=0;
for j:=1 to n do if urn[j]=j then aantal:=aantal+1;
som:=som+aantal;
x:=som/t;
writeln(x:13:10)
end
end.
Looking at the output, I discovered Hn must denote 1+1/2+1/3+...+1/n.
Now how do we calculate the expected value?
E(X) = SUM(j:=1 to n; P(ball j in urn j)) = ...
P(ball 1 in urn 1) = 1/n.
P(ball 2 in urn 2) = 1 - 1/n
P(ball 3 in urn 3) = 1 - P(ball 1 in urn 3) - P(ball 2 in urn 3) = 1 - 1/n - 1/(n(n-1)) = 1 - 1/(n-1)
P(ball 4 in urn 4) = 1 - P(ball 1 in urn 4) - P(ball 2 in urn 4) - P(ball 3 in urn 4) = 1 - 1/n - 1/(n(n-1)) - 1/((n-1)(n-2)) = 1 - 1/(n-2)
P(ball 5 in urn 5) = 1 - P(ball 1 in urn 5) - P(ball 2 in urn 5) - P(ball 3 in urn 5) - P(ball 4 in urn 5) = 1 - 1/n - 1/(n(n-1)) - 1/((n-1)(n-2)) - 1/((n-2)(n-3)) = 1 - 1/(n-3)
... etc.
P(ball j in urn j) = 1 - 1/(n-(j-2))
P(ball n in urn n) = 1 - 1/2
So E(X) = n-1 - (1/2 + 1/3 + .. + 1/(n-1)) = n - Hn-1.
11565 Let U1,U2,... be independent random variables, each uniformly distributed on [0,1].
a) For x in (0,1], let Nx be the least n such that SUM(k from 1 to n:√Uk) is greater than x. Find the expected value of Nx.
b) For x in (0,1], let Mx be the least n such that PRODUCT(k from 1 to n:Uk) is less than x. Find the expected value of Mx.
Solution:
a) (From the output of a Pascal program, I guess E(Nx) must be something like 1+x2, but for larger x a bit more.)
E(Nx) = SUM(n from 1 to ∞: n*P(Nx=n) = P(√u1 > x) + 2*P((√u1 ≤ x) and (√u1+√u2 > x)) + 3*P((√u1+√u2 ≤ x) and (√u1+√u2+√u3 > x)) + 4*P((√u1+√u2+√u3 ≤x) and (√u1+√u2+√u3+√u4 > x)) + ...
= 1-x2 + 2(x2 - INT(u1 from 0 to x2: (x-√u1)2)) + 3(INT(u1 from 0 to x2: (x-√u1)2) - INT(u1 from 0 to x2 and u2 from 0 to (x-√u1)2: (x-√u1-√u2)2)) + 4(INT(u1 from 0 to x2 and u2 from 0 to (x-√u1)2: (x-√u1-√u2)2)) - INT(u1 from 0 to x2 and u2 from 0 to (x-√u1)2 and u3 from 0 to (x-√u1-√u2)2): (x-√u1-√u2-√u3)2)) + ...
= 1 + x2 + INT(u1 from 0 to x2: (x-√u1)2) + INT(u1 from 0 to x2 and u2 from 0 to (x-√u1)2: (x-√u1-√u2)2) + INT(u1 from 0 to x2 and u2 from 0 to (x-√u1)2 and u3 from 0 to (x-√u1-√u2)2): (x-√u1-√u2-√u3)2) + ...
We can calculate these integrals from the inside through the outside by substituting √uk = vk and integrating by parts, and get
1 + x2 + (2/(3*4))x4 + ((2*2)/(3*4*5*6))x6 + ((2*2*2)/(3*4*5*6*7*8))x8 + ... = SUM( n from 0 to ∞: (x√2)2n/(2n)!) = cosh(x√2).
b) E(Mx) = SUM(n from 1 to ∞: n*P(Mx=n)) = P(u1 < x) + 2*P((u1 ≥ x) and (u1*u2 < x)) + 3*P((u1*u2 ≥ x) and (u1*u2*u3 < x)) + 4*P((u1*u2*u3 ≥ x) and (u1*u2*u3*u4 < x)) + ...
= x + 2*INT(u1 from x to 1: x/u1) + 3*INT(u1 from x to 1 and u2 from x/u1 to 1: x/(u1*u2)) + 4*INT(u1 from x to 1 and u2 from x/u1 to 1 and u3 from x/(u1*u2) to 1: x/(u1*u2*u3)) + ...
= x - 2*x*ln(x) +(3/2)*x*ln2(x) - (4/(2*3))*x*ln3(x) + (5/(2*3*4))*x*ln4(x) + ...
= x*SUM(n from 0 to ∞: ((n+1)/(n!))*(-ln(x))n) = ... = 1 - ln(x).
(This agrees with the output of the Pascal program for x=1/e, which seems to fluctuate around 2.)
11570 Alice and Bob play a number game. Starting with a positive number n, they take turns changing the number; Alice goes first.
Each player in turn may change the current number k to either k-1 or roundupward(k/2). The person who changes 1 to 0 wins. For which initial n does Alice have a winning strategy?
Solution:
We find the good n up to N by the following procedure:
good[1]:=true;
for n:=2 to 2*N-2 do good[n]:=false;
for n:=2 to N-1 do if not good[n] then begin good[n+1]:=true; good[2*n-1]:=true; good[2*n]:=true end;
for n:=1 to N do if good[n] then writeln(n,' is good') else writeln(n,' is not good')
11572 Given a circle C and two points A and B outside C, give an Euclidean construction to find a point P on C such that if Q and S are the second intersections with C of AP and BP respectively, then QS is perpendicular to AB. (Special configurations, including the case that A and B and the center of C are collinear, are excluded.)
Partial solution:
(Using Cabri, we can see that such a P does probably exist in most of the cases.)
Let A(a,c), B(b,c), P(cos(t),sin(t)), Q(cos(u),sin(u)), S(cos(u),-sin(u)) (, so AB is perpendicular to QS.)
We must have
1) A,P,Q collinear, which amounts to (cos(t)-a)(sin(u)-c) = (cos(u)-a)(sin(t)-c),
2) B,P,S collinear, which amounts to (cos(t)-b)(-sin(u)-c) = (cos(u)-b)(sin(t)-c).
We can eliminate u from 1) and 2) and find a polynomial p(x) of degree 6 with coefficients expressed in a,b,c such that p(sin(t))=0.
So we have to construct, with compass and straightedge only, the roots of p(x).
But p(x) looks awkward.
11573 A Sudoku Permutation Matrix (SPM) of order n2 is a permutation matrix of order n2 with exactly one 1 in each of the n2 submatrices obtained by partitioning the original matrix into an n-by-n array of submatrices. Thus, for n=2, the permutation 1324 yields an SPM, but the identity permutation 1234 does not. Find the number of SPMs of order n2.
Solution:
First we count the number of SPMs of order n2 with n=2. The outcome is 16.
Next we look at SPMs of order n2 with n=3. Then, generalizing, we see:
The permutation π yields an SPM iff for all k∈{1,2,..n} the sequence π((k-1)n+1), π((k-1)n+2), ..., π(kn), contains exactly one element from each of the n sets
{(k-1)n+1, (k-1)n+2, ..., kn} with k∈{1,2,..n}.
Counting the number of possibilities for π(1), π(2), π(3), ... π(n2), respectively, we find in the end that the number of possible permutations (and hence the number of possible
SPMs) is:
Π(i,j∈{1,2,..,n} : n2-(i+j-2)n+(i-1)(j-1))) = Π(i,j∈{1,2,..n}:(n-(i-1))(n-(j-1))) = (n!)2n. (So this outcome must be less than (n2)!.)
11623 A fair coin is tossed n times and the results recorded as a bit string. A run is a maximal subsequence of identical tosses. Let the random variable Xn be the number of runs in the bit string not immediately followed by a longer run. Find E(Xn).
Solution:
E(Xn) = SUM(k from 1 to n: (n-1 over k-1)*(1+(k-1)*((1/2)*(1-prob)+prob)))/2n-1, where
2n-1 is the number of compositions of n,
(n-1 over k-1) is the number of compositions of n in k parts;
the term 1 counts the last part (which will never be followed by a larger part);
for the other k-1 parts holds that they either will be followed by an equal part (with a chance we denote by prob),
or in half of the cases by a smaller part.
Because SUM(k from 1 to n: (n-1 over k-1)) = 2n-1 and SUM(k from 1 to n: (k-1)*(n-1 over k-1)) = (n-1)*2n-2, we find
E(Xn) = 1 + (n-1)/4 + (1/2n)*SUM(k from 1 to n: (n-1 over k-1)*(k-1)*prob).
In this last sum, the term with k=2 is e/2n where e=1 if n is even and e=0 if n is odd. We find
E(Xn) = 1 + (n-1)/4 + e/2n + (1/2n)*SUM(k from 3 to n: SUM(m from 1 to int((n-(k-2))/2): (k-1)*(n-2m-1 over k-3))), where
(n-2m-1 over k-3) is the number of compositions of n-2m in k-2 parts.
This last doublesum can be calculated by changing the order of summation. With p:=int((n-1)/2) we get
SUM(m from 1 to p: SUM(k from 3 to n-2m+2: (k-1)*(n-2m-1 over k-3))) =
SUM(m from 1 to p: SUM(j from 0 to n-2m-1: (j+2)*(n-2m-1 over j))) =
SUM(m from 1 to p: 2n-2m + (n-2m-1)*2n-2m-2) =
(2n+(n-1)*2n-2)*(1-(1/4)p)/3 - 2n-1*SUM(m from 1 to p: m*(1/4)m), so
E(Xn) = (n+3)/4 + e/2n + ((n+3)/12)*(1-(1/4)p) -(2/9)*(1+p*(1/4)p+1-(p+1)*(1/4)p))
where p:=int((n-1)/2) and e:=1 if n is even and e:=0 if n is odd
(This outcome should be equal to 199/64 for n=7, and it is.)
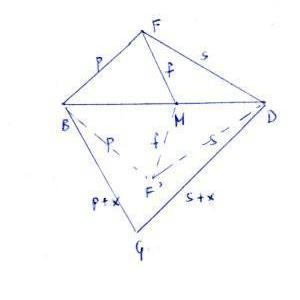
11635 Let ABCD be a convex quadrilateral and M a point on the diagonal BD. Suppose that the perimeters of triangles ABM and BCM are equal, and likewise those of ADM and DCM. Prove that AB = BC and AD = DC.
Solution:
If not, the situation would be like in the following picture (with either (F=A and G=C) or (F=C and G=A)):

where x is positive and, in view of the conditions on the perimeters, GM = f-x.
Then GM is smaller than F'M = f, which is clearly impossible.
(Draw the circles through F' with centers B, M and D; since G is outside the first and the third, it must be outside the second.)
11656 The sign chart of a polynomial f with real coefficients is the list of successive pairs of (f ',f) on the intervals separating real zeros of ff ', together with the signs at the zeros of ff '
themselves, read from left to right.
Thus, for f = x3 - 2x2, the sign chart is ((1,-1),(0,0),(-1,-1),(0,-1),(1,-1),(1,0),(1,1)).
As a function of n, how many sign charts occur for polynomials of degree n?
Partial solution:
We have the following possibilities for a point on the graph of f where the tangent is horizontal:
1) positive local minimum, corresponding to a zero of f ' with odd multipicity;
2) zero local minimum, corresponding to a zero of f ' with odd multipicity;
3) negative local minimum, corresponding to a zero of f ' with odd multipicity;
4) positive reflection point where f is descending, corresponding to a zero of f ' with even multipicity;
5) zero reflection point where f is descending, corresponding to a zero of f ' with even multipicity;
6) negative reflection point where f is descending, corresponding to a zero of f ' with even multipicity;
7) positive reflection point where f is ascending, corresponding to a zero of f ' with even multipicity;
8) zero reflection point where f is ascending, corresponding to a zero of f ' with even multipicity;
9) negative reflection point where f is ascending, corresponding to a zero of f ' with even multipicity;
10) positive local maximum, corresponding to a zero of f ' with odd multipicity;
11) zero local maximum, corresponding to a zero of f ' with odd multipicity;
12) negative local maximum, corresponding to a zero of f ' with odd multipicity;
On the graph of f, if one of these points is followed by another, we have the following posibilities:
A point of kind 1) may be followed by one of kind 10 or 7;
A point of kind 2) may be followed by one of kind 10 or 7;
A point of kind 3) may be followed by one of kind 7 through 12;
A point of kind 4) may be followed by one of kind 1 through 6;
A point of kind 5) may be followed by one of kind 3 or 6;
A point of kind 6) may be followed by one of kind 3 or 6;
A point of kind 7) may be followed by one of kind 10 or 7;
A point of kind 8) may be followed by one of kind 10 or 7;
A point of kind 9) may be followed by one of kind 7 through 12;
A point of kind 10) may be followed by one of kind 1 through 6;
A point of kind 11) may be followed by one of kind 3 or 6;
A point of kind 12) may be followed by one of kind 3 or 6.
Hence we may count the number of sign charts with the following pascal program, using recursion:
(n is the degree of f, g is the maximal degree of a positive definite factor of f ', sommult is the sum of the multiplicities of zeros of f ',
laatste is the last considered point of one of kinds 1) through 12), a is the number of sign charts.)
program opl11656;
var n,m,g,sommult,laatste:integer; a:real;
procedure byzpunten(var sommult,laatste:integer);
var j,k,sm,tm:integer;
begin
sm:=sommult;
if laatste=1 then
begin
for k:=1 to n-1-sm do if (k mod 2)=1 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
laatste:=10; byzpunten(sommult,laatste);
laatste:=7; sommult:=tm; byzpunten(sommult,laatste)
end
end
end;
if laatste=2 then
begin
for k:=1 to n-1-sm do if (k mod 2)=1 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
laatste:=10; byzpunten(sommult,laatste);
laatste:=7; sommult:=tm; byzpunten(sommult,laatste)
end
end
end;
if laatste=3 then
begin
for k:=1 to n-1-sm do if (k mod 2)=1 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
for j:=7 to 12 do
begin sommult:=tm; laatste:=j; byzpunten(sommult,laatste) end;
end
end
end;
if laatste=4 then
begin
for k:=1 to n-1-sm do if (k mod 2)=0 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
for j:=1 to 6 do
begin sommult:=tm; laatste:=j; byzpunten(sommult,laatste) end;
end
;end
end;
;if laatste=5 then
begin
for k:=1 to n-1-sm do if (k mod 2)=0 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
laatste:=3; byzpunten(sommult,laatste);
laatste:=6; sommult:=tm; byzpunten(sommult,laatste)
end
end
end;
if laatste=6 then
begin
for k:=1 to n-1-sm do if (k mod 2)=0 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
laatste:=3; byzpunten(sommult,laatste);
laatste:=6; sommult:=tm; byzpunten(sommult,laatste)
end
end
end;
if laatste=7 then
begin
for k:=1 to n-1-sm do if (k mod 2)=0 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
laatste:=10; byzpunten(sommult,laatste);
laatste:=7; sommult:=tm; byzpunten(sommult,laatste)
end
end
end;
if laatste=8 then
begin
for k:=1 to n-1-sm do if (k mod 2)=0 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
laatste:=10; byzpunten(sommult,laatste);
laatste:=7; sommult:=tm; byzpunten(sommult,laatste)
end
end
end;
if laatste=9 then
begin
for k:=1 to n-1-sm do if (k mod 2)=0 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
for j:=7 to 12 do
begin sommult:=tm; laatste:=j; byzpunten(sommult,laatste) end;
end
end
end;
if laatste=10 then
begin
for k:=1 to n-1-sm do if (k mod 2)=1 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
for j:=1 to 6 do
begin sommult:=tm; laatste:=j; byzpunten(sommult,laatste) end;
end
;end
end;
if laatste=11 then
begin
for k:=1 to n-1-sm do if (k mod 2)=1 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
laatste:=3; byzpunten(sommult,laatste);
laatste:=6; sommult:=tm; byzpunten(sommult,laatste)
end
end
end;
if laatste=12 then
begin
for k:=1 to n-1-sm do if (k mod 2)=1 then
begin
sommult:=sommult+k;
if sommult=n-1 then a:=a+1 else
begin
tm:=sommult;
laatste:=3; byzpunten(sommult,laatste);
laatste:=6; sommult:=tm; byzpunten(sommult,laatste)
end
end
end;
end{byzpunten};
begin
for n:=1 to 30 do
begin
if ((n-1) mod 2)=0 then a:=1 else a:=0;
for g:=0 to n-2 do if (g mod 2)=0 then
for m:=1 to 6 do
begin sommult:=g; laatste:=m; byzpunten(sommult,laatste) end;
a:=2*a; writeln(n:4,a:13:0)
end
end.
The output comes quickly for n from 1 through 20, slowly for n from 21 through 23, and too slowly or not at all for n at least 24.
The results (n,a) are as follows:
(1,2), (2,6), (3,18), (4,48), (5,128), (6,336), (7,882), (8,2310), (9,6050), (10,15840), (11,41472), (12,108576), (13,284258), (14,744198), (15,1948338), (16,5100816),
(17,13354112), (18,34961520), (19,91530450), (20,239629830), (21,627359042), (22,1642447296), (23,4299982848), (24,11257501248), (25,29472520898), ...
I discovered, denoting the a that belongs to n by an:
if a2m+1/a2m = p/q (lowest terms), then both a2m+2/a2m+1 and a2m+3/a2m+2 are equal to (p2-1)/(pq).
The sequence of factors 3, 8/3, 21/8, 55/21, 144/55, 377/144, 987/377, ... seems to tend to 2.618... = (3+√5)/2.
We now see that the sequence an begins as follows:
2*1*1, 2*1*3, 2*3*3, 2*3*8, 2*8*8, 2*8*21, 2*21*21, 2*21*55, 2*55*55, 2*55*144, 2*144*144, 2*144*377, 2*377*377, 2*377*987, ...
Here we can decompose the sequence 1,3,8,21,55,144,377,987, ... as follows: 1*1, 1*3, 2*4, 3*7, 5*11, 8*18, 13*29, 21*47, ... so it is the product of two Fibonacci sequences.
If we denote by F the Fibonacci sequence 1,1,2,3,5,8,13,21, ... and by G the Fibonacci sequence 1,3,4,7,11,18,29,47, ...
and by x the product with xm:=Fm*Gm,
then we find xm=F2m and (for these low values of m):
a2m-1 = 2*xm*xm and a2m = 2*xm*xm+1.
To prove with induction that this holds for all natural m, we still need some combinatorial argument that explains why for all natural m should hold
a2m+1/a2m = a2m/a2m-1 = F2m+2/F2m.
(O.P.Lossers suggests the sequence is also generated by the recurrence an+1 - an-1 = 2F2n.)
Earlier solutions 1: click here .
Earlier solutions 2: click here .
Earlier solutions 3: click here .
Earlier solutions 4: click here .
Earlier solutions 5: click here .
More solutions: click here