11718 Given positive real numbers a1,a2,..,an with n≥2, minimize Σxi subject to the condition that x1,x2,.., xn are positive and that Πxi = Σaixi.
Solution:
Since, by Lagrage's rule, there must be some scalar λ such that Π(i≠k)xi - ak = λ for all k, and hence Πxi - akxk = λxk for all k, we find, using Πxi = Σaixi:
(-λ)x1 + a2x2 + ... + anxn = 0,
a1x1 + (-λ)x2 + ... + anxn = 0,
... ,
a1x1 + a2x2 + ... + (-λ)xn = 0.
(As a consequence, λΣxi = (n-1)Σaixi = (n-1)Πxi and λ must be positive.)
So we can find x1, ... , xn by first finding a positive λ that makes the determinant of the matrix of coefficients 0,
then solving the system of linear equations, and finally using λΣxi = (n-1)Πxi.
Here, the determinant is 0 iff
(*) λn = λn-2Σaiaj + 2λn-3Σaiajak +
... + tλn-t-1Σai1ai2..ai(t+1) + ... +(n-1)a1a2..an
Of course we can find λ up to machine uncertainty with the procedure
begin λ:=0; repeat λ := λ + 0.00...01 until (*) end.
For n=2 we find: λ = √(a1a2) and x1 = a2 + √(a1a2), x2 = a1 + √(a1a2).
For n=3 we find, using Cardano's formula:
λ = ∛(a1a2a3 + √(a12a22a32 -
(a1a2+a1a3+a2a3)3/27)) +
∛(a1a2a3 - √(a12a22a32 -
(a1a2+a1a3+a2a3)3/27)).
In general we find with a bit of sweeping:
x1 = x,
xm = x(λ+a1)/(λ+am) for m > 1.
Then, using λΣxi = (n-1)Πxi, we find:
xm = ((λ/(n-1)).(Σ(k from 1 to n) Π(j not k) (λ+aj)))1/(n-1)/(λ+am).
Σxm = ((n-1)/λ)Πxm = (λ/(n-1))1/(n-1)(Σ(k from 1 to n) Π(j not k) (λ+aj))n/(n-1)/Π(λ+ai).
Now, using P(λ) := Π(λ+ai) and its derivative P'(λ) = Σ(k from 1 to n) Π(j not k) (λ+aj), and (*), we find after a bit of calculation
Σxm = ((n-1)/λ) P(λ)1/(n-1).
Notice that if all am are equal to a, then the solution is given by λ = (n-1)a and xm = (na)1/(n-1).
11719 Let f be a twice-differentiable function from [0,∞) into (0,∞) such that f "(x)/(f(x)(1 + f '(x)2)2) tends to ∞ if x tends to ∞.
Show that the product of the integrals ∫0x √(1 + f '(t)2)/f(t) dt and ∫x∞ √(1 + f '(t)2)f(t) dt
tends to 0 if x tends to ∞.
Partial solution:
We restrict ourselves to the special case f(x) = ep(x), where p(x) is a polynomial.
In this case, the condition is satified iff p(x) has degree n ≥ 2 and its coefficient of xn is negative, which we henceforth assume.
Then √(1 + f '(t)2) has a maximum on [0,∞), so we need only prove that the product of the integrals ∫0x 1/f(t) dt and
∫x∞ f(t) dt tends to 0 if x tends to ∞.
To do this, we apply the theorems of l'Hôpital several times, and find eventually that the assertion is true if 1/(-p"(x)+p'(x)2) tends to 0 if x tends to ∞.
Since this holds under our assumptions, we are finished in our special case.
11720 Let En(t) be the Eulerian polynomial defined by En(t) := (1-t)n+1 Σk=0∞ (k+1)ntk,
and let Bn be the n-th Bernouilli number.
Show that Bn(En+1(t) - (1-t)n) is a polynomial with integer coefficients.
Solution:
It is well known that for odd n > 1 holds Bn = 0. So in these cases the assertion is true.
Starting with Σk=0∞ tk = 1/(1-t), by repeatedly multiplying with t and differentiating the resulting power series, we find:
En+1 = (1+nt)En + (t-t2)En',
so if En = 1 + a1t + a2t2 + ... + a2tn-3 + a1tn-2 + tn-1 then
En+1 = 1 + (2a1+n)t + (3a2+(n-1)a1)t2 + (4a3+(n-2)a2)t3 + ...
+ (4a3+(n-2)a2)tn-3 + (3a2+(n-1)a1)tn-2 + (2a1+n)tn-1 + tn,
and:
En = 1 for n=1, 1+t for n=2, 1+4t+t2 for n=3, 1+11t+11t2+t3 for n=4, 1+26t+66t2+26t3+t4 for n=5,
1+57t+302t2+302t3+57t4+t5 for n=6,
1+120t+1191t2+2416t3+1191t4+120t5+t6 for n=7, ...
Furthermore we use the defining formula Bn+1 = Σj=0n+1 (n+1 over j) Bj.
We find (n+1)Bn = - Σj=0n-1 (n+1 over j) Bj, and hence:
B1= -1/2, B2 = 1/6, B3 = 0, B4 = -1/30, B5 = 0, B6 = 1/42, B7 = 0, ...
I read in the Wolfram site the denominator of Bn with even n is the product of the primes p for which p-1 divides n.
Now we readily find Bn(En+1(t) - (1-t)n) = -t for n=1, t for n=2, 0 for n=3, -t-2t2-t3 for n=4, 0 for n=5, 3t+28t2+58t3+28t4+3t5 for n=6, 0 for n=7, ...
We see the coefficients of tk and tn-k in En+1 are equal, for k=0 they are 1 and for k=1 they are Σk=0n k*2n-k = 2n+1-n-2.
So the coefficients of tk and tn-k in En+1 - (1-t)n are equal too, for k=0 they are 0 and for k=1 they are 2n+1-2.
It turns out that the coefficients of tk and tn-k in En+1 all have the form
(-1)k(n over k) + Σj=2k+1 (jn+1-j) pj(n), where pj(n) is a polynomial in n with integer coefficients.
Hence, because of Fermat's little theorem, these coefficients are divisible by the primes p for which p-1 divides n.
11722 Let ABC be an acute triangle in the plane, and let M be a point inside ABC. Let O1, O2, O3 be the circumcenters of BCM, CAM and ABM, repectively.
Let c be the circumcircle of ABC. Let D, E, F be the points opposite A, B and C, respectively, at which AM, BM and CM meet c.
Prove that DO1, EO2 and FO3 are concurrent at a point P that lies on c.
Solution:
We give coordinates such that c has equation x2 + y2 = 1 and A(cos(ρ),sin(ρ)), B(cos(σ),sin(σ)), C(cos(τ),sin(τ)) and M(r,0).
After a bit of calculation we find D(d1/d, d2/d) and O1(o11/o1, o12/o1) where
d1 = 2r - (1+r2)cos(ρ), d2 = (r2-1)sin(ρ), d = r2 - 2r cos(ρ) + 1, and
o11 = (1-r2)(sin(σ) - sin(τ)), o12 = (1-r2)(cos(τ) - cos(σ)), o1 = 2r(sin(τ) - sin(σ)) - 2sin(τ - σ).
Now we easily find the coordinates of E, O2, F, O3, too.
We may also calculate the second intersection points P, Q, R of c and, respectively, DO1, EO2 and FO3. (We use d12 + d22 = d2, and likewise for E and F).
By the symmetry between ρ, σ and τ in the coordinates of P, we see already that Q and R must coincide with P.
For instance, after cancellations using goniometrical formulas, the coefficient of r6 in the numerator of the first coordinate turns out to be cos(ρ+σ+τ).
11723 Let A,B,C be three points in the plane, and let D,E,F be points lying on BC,CA,AB, repectively. Show there exists a conic tangent to BC,CA,AB at D,E,F, respectively, if and only if AD,BE,CF are concurrent.
Solution:
The assertion is clearly true if A,B,C are collinear, so henceforward we suppose they aren't.
Let a:=BC, b:=AC and c:=AB.
Let j be the conic of lines (conic of tangents) to which a,b,c belong and with contact points D on a and E on b.
Let X be the contact point of j on c.
According to the theorem of Pascal (or Brianchon), applied to ((abc)(cab)), the lines a.a-b.c = DA, b.b-c.a = EB and c.c-a.b = XC are concurrent at a point P.
This point P must be DA.EB, so X is the intersection point of PC and c.
Now if DA,EB and FC are concurrent, then PC.c = F and the conic J with corresponding conic of tangents j satisfies the conditions.
On the other hand, if there is a conic J that meets the conditions, its corresponding conic of tangents must be j, and according to Pascal (Brianchon), the lines DA,EB,FC are concurrent.
11724 Let f(n) = Σk=1n kk and let g(n) = Σk=1n f(k).
Find limn → ∞ g(n+2)/g(n+1) - g(n+1)/g(n).
Partial solution:
I ran the following pascal program:
program p11724;
var k:integer; f,g0,g1,r0,r1:real;
begin
g0:=1; g1:=6;
k:=2; f:=5;
r1:=6;
while true do
begin
r0:=r1; k:=k+1;
f:=f+exp(k*ln(k));
g0:=g1;
g1:=g1+f;
r1:=g1/g0;
writeln(r1-r0:13:5);
readln
end
end.
It seems the outcome tends to the well known transcendental number e = 2.71828...
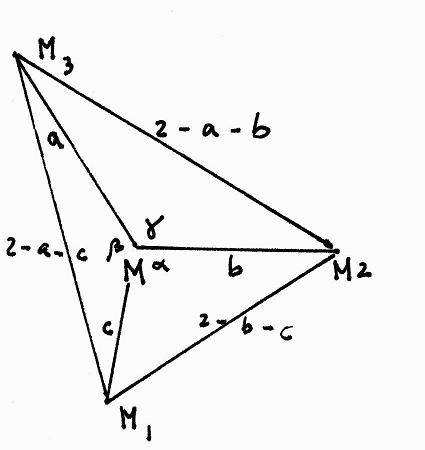
11727 Let R be a circle with center M. Let R2 and R3 be circles with centers M2 and M3 inside R, such that R2 and R3
are externally tangent and both are internally tangent to R.
Give a straightedge and compass construction of the circle R1 that is internally tangent to R and externally tangent to R2 and R3.
Solution:
See the following figure. Here a and b and γ are given, and we have to construct c.

This can be done as follows:
1) Using the cosine rule we find cos(α) = (2b+2c-2-bc)/(bc), cos(β) = (2a+2c-2-ac)/(ac), cos(γ) = (2a+2b-2-ab)/(ab).
2) Since α + β + γ = 2*π, we have 2 cos(α) cos(β) cos(γ) = cos2(α) + cos2(β) + cos2(γ) -1.
3) Combining 1) and 2), we find the following quadratic equation with unknown c:
c2(-a2b2+4a2b+4ab2-4a2-4b2-10ab+8a+8b-5) + c(4a2b2-10a2b-10ab2+8a2+8b2+20ab-14a-14b+8) + (-4a2b2+8a2b+8ab2-5a2-5b2-14ab+8a+8b-4) = 0.
4) Hence we can solve the equation in 3) and construct c.
The discriminant is
16(a4b3+a3b4-7a3b3-3a4b2-3a2b4+3a4b+3ab4+15a3b2
+15a2b3-a4-b4-13a3b-13ab3-27a2b2+4a3+4b3+21a2b+21ab2-6a2
-6b2-15ab+4a+4b-1), which is not the square of a polynomial p(a,b).
So for both possible solutions a construction procedure involves the construction of the square root of the discriminant.
11729 An integer is called b-normal if all digits 0,1,..,b-1 appear the same number of times in the base-b expansion of n. Let N(b) be the set of all b-normal integers. Determine those b for which Σn ∈ N(b) 1/n < ∞.
Solution:
Any b-normal integer in which the digits appear t times lies between Σk=0b-1 (b-k-1)btk(1+b+...+bt-1) + btb-1 - btb-t-1
and Σk=0b-1 kbtk(1+b+...+bt-1).
Hence we see after a bit of calculation that any b-normal integer in which the digits appear t times is greater than btb-1 and smaller than btb.
There are (tb)!/(t!)b such integers, given t and b.
So Σn ∈ N(b) 1/n is greater than Σt=1∞ ((tb)!/(t!)b)b-tb and smaller than
Σt=1∞ ((tb)!/(t!)b)b1-tb.
According to Stirling, the general term of each of these last two series is comparable to t(1-b)/2.
Therefore the answer is: for b > 3.
11731 The integer simplex with dimension d and side-length m is the graph T(d,m) whose vertices are the non-negative (d+1)-tuples summing to m, with two vertices adjacent when they differ by 1 in two
places and are equal in all other places.
Determine the connectivity, the chromatic number, and the edge-chromatic number of T(d,m) (the latter when m > d).
First approach (after studying T(2,3)):
Any such (d+1)-tuple in which k coordinates are equal to 0 and d+1-k coordinates positive is connected with k(d+1-k) + 2(d+1-k over 2) = d(d+1-k) other vertices.
I guess the connectivity is the minimum d of d(d+1-k), which is attained for k=d, and the edge-chromatic number is the maximum d(d+1) of d(d+1-k), attained for k=0.
11732 Let a and b be real numbers with 1 < a < b and let m and n be real numbers and m not 0.
Find all continuous real functions f with domain [0,∞) such that for all x ≥ 0 holds f(ax) + f(bx) = mx+n.
Solution:
Let b = as, so s = ln(b)/ln(a) > 1.
Let's first restrict ourselves to the case that f(ax) is a linear function, so we're looking for some real numbers c and d such that
f(ax) = c + dx and f(bx) = c + dsx for all x≥0.
In this case, f(ax) + f(bx) = mx + n for all nonnegative x if and only if 2c = n and d(s+1) = m, so c = n/2 and d = m ln(a)/ln(ab).
Next we examine the general case: we're seeking all functions g(x) such that f(ax) = n/2 + m ln(a)/ln(ab) x + g(x) satisfies the requirements.
Such a g:[0,∞) → ℜ has to be continuous and, with our s>1, it has to satisfy g(sx) = - g(x) for all x in [0,∞).
But then g(x) = 0 for all x in [0,∞), because if there would exist a c for which g(c) is not 0, then (-1)kg(c) = g(c/sk) would tend to g(0) if k → ∞, which is
clearly a contradiction.
We conclude that any continuous function f with domain [0,∞) will do if and only if for all t = ax ≥ 1 we have f(t) = n/2 + m ln(t)/ln(ab).
11734 Find all lists (a,k,m,n) of positive integers such that am+n + an - am - 1 = 15k.
Partial solution:
The solutions with k=1 are (4,1,1,1) and (2,1,2,2).
With Pascal I didn't find other solutions (for k:=1 to 8 do for a:=1 to 20 do for n:=1 to k+2 do for m:=1 to k+3-n do)
Suppose (a,k,m,n) is a solution with k>1.
Then the right hand side has exactly k prime factors 3 and exactly k prime factors 5 and no other prime factors, so this holds for the left hand side as well.
Now the left hand side is equal to (a - 1)(1 + a + a2 + ... + an-1)(am + 1), so for some nonnegative integers i,j we have a = 1 + 3i5j.
Then the left hand side is equal to 3i5j(n + (n over 2) 3i5j + (n over 3) 32i52j + ... + 3(n-1)i5(n-1)j)
(2 + m 3i5j + (m over 2) 32i52j + ... + 3mi5mj).
If i and j are both positive, then (2 + m 3i5j + (m over 2) 32i52j + ... + 3mi5mj)
has a prime factor different from 3 and different from 5, so this isn't possible.
If i is positive and j=0 then we find
3i(n + (n over 2) 3i + (n over 3) 32i + ... + 3(n-1)i)
(2 + m 3i + (m over 2) 32i + ... + 3mi) = 3k5k, so (2 + m 3i + (m over 2) 32i + ... + 3mi) is a power of 5.
If i=0 and j is positive then we find
5j(n + (n over 2) 5j + (n over 3) 52j + ... + 5(n-1)j)
(2 + m 5j + (m over 2) 52j + ... + 5mj) = 3k5k, so (2 + m 5j + (m over 2) 52j + ... + 5mj) is a power of 3.
If i and j are both 0, then a=2 and (2n - 1)(2m + 1) = 15k.
Because (an-1)(am+1) = (-1)k modulo 16 and a = 1 + 3i5j, we see by considering the powers of 3 (mod 16) and those of 5 (mod 16)
that in all remaining cases where i and j aren't both positive, k must be odd.
(If a=2 and n=1 we have 2m + 1 = 15k, which is impossible since 2m + 1 can't be divisible both by 3 and by 5.)
11735 Let P be a point inside triangle ABC. Let dA and dB and dC be the distances from P to A and B and C, respectively.
Let rA and rB and rC be the radii of the circumcircles of PBC and PCA and PAB, respectively.
Prove that 1/dA + 1/dB + 1/dC ≥ 1/rA + 1/rB + 1/rC .
Partial solution:
Give coordinates P(0,0), A(dA ,0), B(dB cos(s), dB sin(s)), C(dC cos(t), -dC sin(t)), with 0 < min(s,t) ≤ max(s,t) < π < s+t.
Then we find rA = √(dB2 + dC2 - 2dB dC cos(s+t)) / |2 sin(s+t)|, rB = √(dA2 + dC2 - 2dA dC cos(t)) / (2 sin(t)), rC = √(dA2 + dB2 - 2dA dB cos(s)) / (2 sin(s)).
We could check the inequality by comparing its left side and its right side for, say, 18021003 elements
(s,t,dA,dB,dC) ∈ {0 < min(s,t) ≤ max(s,t) < π < s+t, 0 < dA,dB,dC ≤ 1}
with the help of a computer program.
There is equality if dA = dB = dC and s = t = 2π/3.
11737 Given an acute triangle ABC, let O be its circumcenter, let M be the intersection of the lines AO and BC, and let D be the other intersection of AO with the circumcircle of ABC.
Let E be that point on AD such that M is the midpoint of ED. Let F be the point at which the perpendicular to AD at M meets AC.
Prove that EF is perpendicular to AB.
Solution:
Give coordinates O(0,0), A(1,0), B(cos(σ),sin(σ)), C(cos(τ),sin(τ)), with 0 < σ < π and π < τ <σ + π.
Then we find M(sin(σ-τ)/(sin(σ)-sin(τ)),0), D(-1,0), E(1 + 2 sin(σ-τ)/(sin(σ)-sin(τ)),0),
F(sin(σ-τ)/(sin(σ)-sin(τ)), ((sin(σ-τ) - sin(σ) + sin(τ)) sin(τ))/((sin(σ) - sin(τ))(cos(τ) - 1))).
Now, using trigonometric identities, it's straightforward to show that the inner product of the direction vectors of EF and AB is zero.
11738 Three point particles are constrained to move without friction along a unit circle. Three ideal massless springs of stiffness k1, k2 and k3 connect the particles
pairwise.
Show that an equilibrium in which the particles occupy three distinct positions exists if and only if 1/k1, 1/k2 and 1/k3 can be the lengths of the sides of a triangle.
Show also that if this happens, the equilibrium length L1 of the spring with stiffness k1 is given by L1 =
√(k2k3) √((1/k2 + 1/k3)2 - 1/k12).
Partial solution:
From the last assertion it is clear what L2 and L3 should be. We will try and prove only this second assertion, because it clearly implies the first one.
To find a symmetric relation involving ki and Li (i=1,2,3) that is as simple as possible and doesn't contain square roots, we intuitively calculate
k1L12 + k2L22 + k3L32 with the proposed values of Li, and find it is equal to
k1k2k3(1/k1 + 1/k2 + 1/k3)2.
So, although I don't know the physics implied in this problem, I guess these physics demand that exactly this relation be satisfied:
k1L12 + k2L22 + k3L32 =
k1k2k3(1/k1 + 1/k2 + 1/k3)2.
Then it follows that Li is as proposed (i=1,2,3).
(I think the proposer of the problem forgot to multiply the three equilibrium lengths with a constant so as to get L1 + L2 + L3 = 2π,
or else it isn't clear how he defines a 'unit circle'.)
11739 Let B(x) be the 2x2 matrix whose diagonal elements are 1 and whose offdiagonal elements are x. Evaluate the infinite matrix product M = Πp B(p-2), where the product runs over all primes in increasing order.
Partial solution:
M is the 2x2 matrix whose diagonal elements are equal to 1 + Σ(p1p2)-2 + Σ(p1p2p3p4)-2 + ...
and whose offdiagonal elements are equal to Σp1-2 + Σ(p1p2p3)-2 +
Σ(p1p2p3p4p5)-2 + ... ,
where each sum is for some fixed nonnegative integer k taken over all k-tuples of distinct primes p1 < p2 < ... < pk.
I think the values of these sums, involving zeta functions, can be found somewhere in the mathematical literature.
Earlier solutions 1: click here .
Earlier solutions 2: click here .
Earlier solutions 3: click here .
Earlier solutions 4: click here .
Earlier solutions 5: click here .
Earlier solutions 6: click here .
Earlier solutions 7: click here .