DIFFERENTIAL GEOMETRY COURSE
5.CURVATURE AND TORSION
Explanation 42: We can give a proof analogous to the one in explanation 22 of:
τ(s)2 = lim (Δs→0) (Δψ/Δs)2,
where Δψ is the angle between the binormals
in s and s+Δs.
Here we use ||b .(s)||2 = τ(s)2 (see proposition 38).
Explanation 43: According to Taylor we have x(s) = x(s0) + (s-s0)x .(s0) +
(1/2)(s-s0)2x ..(s0) + (1/6)(s-s0)3x ...(s0) + O(s-s0)4
= x(s0) + ht + (1/2)h2κn + (1/6)h3(κ .n+
κ(-κt+τb)) + ...
If we choose x(s0) as origin, then the coordinates of x(s) with respect to (t,n,b) are in approximation:
α = h - (1/6)κ2h3, β = (1/2)κh2 + (1/6)κ . h3, γ =
(1/6)κτh3.
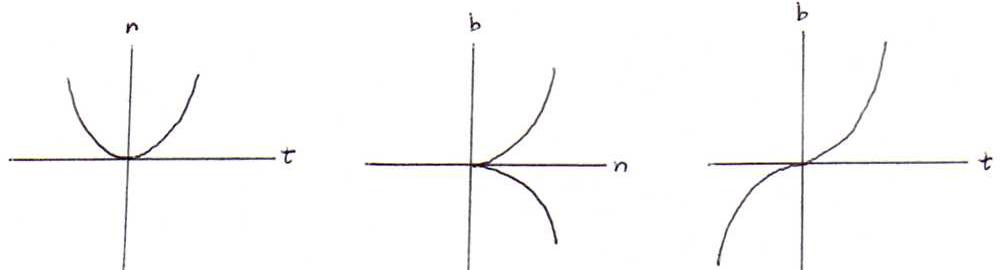
So the projection on the osculating plane is in approximation the parabola (h,(1/2)κh2). This gives us a geometric insight in curvature.
The projection on the normal plane is in approximation the cubic parabola (β,+((τ√2)/(3√κ))β3/2). This gives us a geometric insight in torsion.
The projection on the rectifying plane is in approximation the cubic curve (α,(1/6)κτα3).

Proposition 44: The planar curves are exactly the curves with torsion 0.
Prove: Suppose τ=0. Then b . = 0, so b is constant.
The osculating plane has equation x.b = a(s) where a(s) = x(s).b.
Then a .(s) = t(s).b = 0, so a is constant. So the curve is lying in the plane x.b = a.
On the other hand, every planar curve has torsion 0, because the binormal is constant (normal vector of length 1 perpendicular to the plane of the curve).
Problem 45:Let d = ||x(s) - x(s0)|| and h = s-s0.
Prove with the help of explanation 43 that lim (h→0) (h-d)/h3 = κ(s0)2/24. Give a geometric interpretation.
Problem 46: Prove that the circular helix (see 11 ii) ) has constant curvature and constant torsion.
Problem 47: Calculate κ(t) and τ(t) of the following curves (use 20,40,41) :
i) x(t) = (a(t-sin(t)), a(1-cos(t)), 4b*cos(t/2));
ii) y(t) = (3cos(t)+3t*sin(t), 3sin(t)-3t*cos(t), 2t2);
iii) z(t) = (6t, 3t2, t3).
These are there examples of helices (but not circular), of which we will speak further later on.
Problem 48: Calculate the arc length s of the conic curve in problem 19: x(t) = a*ect(cos(t),sin(t),1). Subsequently, explain how we can calculate κ(s) and τ(s).
Proposition 49: Every curve is uniquely determined by its curvature function and its torsion function, up to a stiff motion in space.
Explanation50: This follows from a theorem about differential equations, when we apply them on the formulas of Serret and Frenet. This theorem says that under certain conditions n equations with n unknown variables have exactly 1 solution (up to integration constants).
In the following sections we will see examples where a certain sort of curves is characterised by an equation involving κ and/or τ.
In general, a system of two such equations determines the curve. (Then we call them 'natural equations' of the curve.)
Problem 51: Suppose the principle normals of a curve go through a fixed point. Prove that the curve is a circle.