CURSUS DIFFERENTIAALMEETKUNDE
22. TOT SLOT
De volgende en laatste stelling is een vereenvoudigde versie van de bekende stelling van Gausz en Bonnet.
Deze laatste is verwant aan de stellingen van Gausz, Stokes en Green in de Analyse.
De inhoud van de stelling van Gausz en Bonnet was al bekend aan Carl Friedrich Gausz (1777-1855), maar werd pas bewezen door O.Bonnet (1819-1892).
Stelling 193: Gegeven drie punten op een oppervlak. Zij G de geodetische driehoek begrensd door de kortste-weg-geodeten tussen deze drie punten. Dan is de oppervlakte-integraal van de totale kromming
over G gelijk aan het hoekexces α + β + γ - π (α, β, γ zijn de hoeken tussen de raaklijnen aan de geodetische zijden van deze driehoek in de hoekpunten).
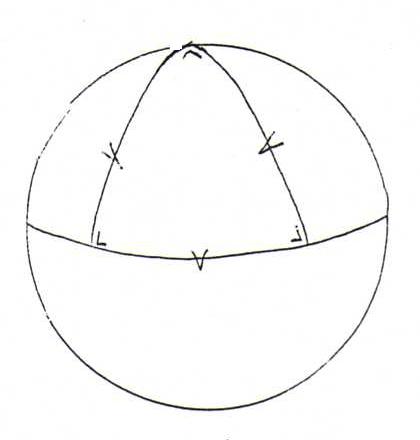
Voorbeeld 194: Op een bol met straal R is de totale kromming in elk punt 1/R2. De oppervlakte van een geodetische driehoek met drie rechte hoeken, een hoekpunt op de noordpool en
twee op de evenaar, is 4πR2/8, terwijl het hoekexces gelijk is aan 3π/2-π. Hier is dus voldaan aan de stelling van Gausz en Bonnet.

Zie hier een algemenere behandeling van het hoekexces op een bol.
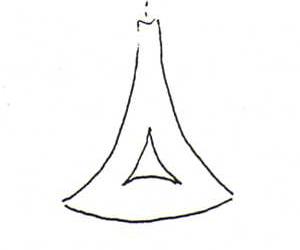
Opmerking 195: Het omwentelingsoppervlak van de tractrix heeft een constante negatieve kromming, en heet daarom 'pseudo-bol'.
Een geodetische driehoek op deze pseudo-bol heeft dus altijd een negatief hoekexces.
Zie hier een oppervlakkige behandeling van de rol die bol en pseudo-bol spelen in de niet-euclidische meetkunde.
Opmerking 196: De tractrix (sleepkromme) kwamen we al tegen in 153.
Parametrisering is (u,0,f(u)) met f(u) = + ∫cu √(c2-y2)/y dy.
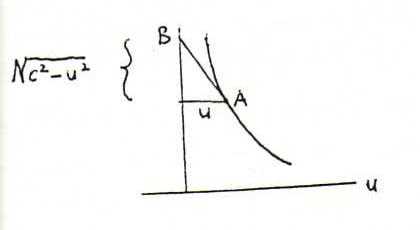
(Hier is d(A,B)=c; ga na dat de grafiek van f de baan is van een hond die op constante afstand c achter een haas aan blijft rennen die over de y-as vlucht.)
Opgave 197: Reken na dat de totale kromming van de pseudo-bol constant gelijk is aan -1/c2.