5.KROMMING EN TORSIE

Toelichting 42: Analoog aan toelichting 22 bewijst men:
τ(s)² = lim (Δs→0) (Δψ/Δs)², waarbij Δψ de hoek is tussen de binormalen in s en s+Δs.
Hierbij gebruikt men ||b ^.(s)||² = τ(s)² (zie stelling 38).

Toelichting 43: Volgens Taylor is x(s) = x(s₀) + (s-s₀)x ^.(s₀) + (1/2)(s-s₀)²x ^..(s₀) + (1/6)(s-s₀)³x ^...(s₀) + O(s-s₀)⁴ = x(s₀) + ht + (1/2)h²κn + (1/6)h³(κ ^.n+ κ(-κt+τb)) + ...
Kiest men x(s₀) als oorsprong, dan zijn de coördinaten van x(s) ten opzichte van (t,n,b) bij benadering:
α = h - (1/6)κ²h³, β = (1/2)κh² + (1/6)κ ^. h³, γ = (1/6)κτh³.

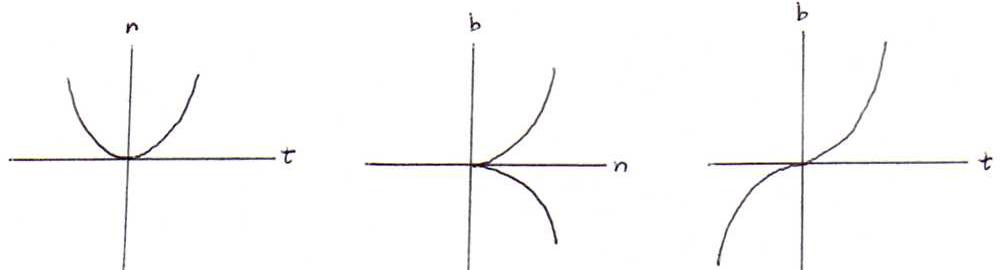
De projectie op het osculatievlak is dus bij benadering de parabool (h,(1/2)κh²). Dit geeft een meetkundig inzicht in de kromming.

De projectie op het normalenvlak is bij benadering de kubische parabool (β,+((τ√2)/(3√κ))β^3/2). Dit geeft een meetkundig inzicht in de torsie.

De projectie op het rectificerend vlak is bij benadering de derdegraadskromme (α,(1/6)κτα³).

Stelling 44: De vlakke krommen zijn precies de krommen met torsie 0.

Bewijs: Stel τ=0. Dan b ^. = 0, dus b is constant.
Het osculatievlak heeft vergelijking x.b = a(s) met a(s) = x(s).b.
Dan is a ^.(s) = t(s).b = 0, dus a is constant. De kromme ligt dus in het vlak x.b = a.
Omgekeerd heeft elke vlakke kromme torsie 0, omdat de binormaal constant is (eenheidsnormaal op het vlak van de kromme).

Opgave 45: Zij d = ||x(s) - x(s₀)|| en h = s-s₀.
Bewijs met behulp van toelichting 43 dat lim (h→0) (h-d)/h³ = κ(s₀)²/24. Interpreteer dit meetkundig.

Opgave 46: Bewijs dat de cirkelschroeflijn (zie 11 ii) ) constante kromming en torsie heeft.

Opgave 47: Bereken κ(t) en τ(t) voor de volgende krommen (werk met 20,40,41) :
i) x(t) = (a(t-sin(t)), a(1-cos(t)), 4b*cos(t/2));
ii) y(t) = (3cos(t)+3t*sin(t), 3sin(t)-3t*cos(t), 2t²);
iii) z(t) = (6t, 3t², t³).
Dit zijn alle drie voorbeelden van schroeflijnen (geen cirkelschroeflijnen), waarover later meer.

Opgave 48: Bereken de booglengte s voor de kegelkromme van opgave 19: x(t) = a*e^ct(cos(t),sin(t),1). Geef vervolgens aan hoe men κ(s) en τ(s) kan berekenen.

Stelling 49: Elke kromme is door zijn krommingsfunctie en zijn torsiefunctie eenduidig bepaald tot op een starre ruimtelijke beweging na.

Toelichting 50: Dit volgt uit een stelling over differentiaalvergelijkingen, toegepast op de formules van Serrat en Frenet. Deze stelling zegt dat onder bepaalde voorwaarden n vergelijkingen met n onbekenden precies 1 oplossing hebben (op integratieconstanten na).

In de volgende paragrafen zullen we voorbeelden zien waarbij telkens een bepaald soort krommen gekarakteriseerd wordt door een vergelijking waar κ en/of τ in voorkomen.
Een stelsel van twee zulke vergelijkingen bepaalt in het algemeen de kromme (dit heten dan 'natuurlijke vergelijkingen' van de kromme).

Opgave 51: Bewijs dat, indien de hoofdnormalen van een kromme door een vast punt gaan, deze kromme een cirkel is.

uitwerkingen