CURSUS GRONDSLAGEN VAN DE MEETKUNDE
HOOFDSTUK ACHT
Het systeem van Euclides-Hilbert is aanvankelijk niet 'metrisch', maar 'synthetisch': de begrippen afstand en hoekmaat hebben er in het begin geen plaats.
De axioma's voor een synthetische opbouw zijn, voor de theorie die we tot nu toe besproken hebben:
In1 t/m In4 (over de incidentie); B1 t/m B5 (over 'tussen') en C1 t/m C5 (over congruentie van segmenten) (,deze laatste tien hebben we in het metrische
systeem afgeleid als stellingen, mbv het afstandsbegrip en Dis1); HV; C6 t/m C9 (,dit zijn de beweringen die in opgave 8 mbv het hoekmaatbegrip als stellingen van het metrische
systeem mbv M1 t/m M4 bewezen zijn); ZHZ.
Stel dat we willen overstappen op het synthetische systeem (Euclides deed ook niet aan metriek). Wat moeten we dan opnieuw doen of aanvullen?
1) Stelling 5.2 over congruentie van overstaande hoeken bewijzen.
2) Bewijzen dat alle rechte hoeken congruent zijn.
3) Bewijzen dat door een punt P op een lijn l een loodlijn m gaat.
4) Een vervangende formulering vinden voor de stellingen 7.3 en 7.4 (mbt de driehoeksongelijkheid), en deze opnieuw bewijzen.
Verder niets.
1) In het bewijs van stelling 5.2 kan de volgende stelling dienen om de hoekmeting te elimineren:
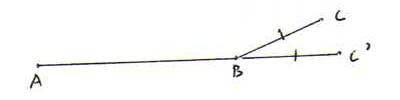
Stelling 8.1 : Als ∠BAC en ∠CAD een lineair paar vormen en ∠B'A'C' en ∠C'A'D' een lineair paar vormen en ∠CAD ≅ ∠C'A'D', dan ∠BAD ≅ ∠B'A'D'.
Bewijs: Zonder verlies van algemeenheid nemen we aan dat [BA] ≅ [B'A'], [CA] ≅ [C'A'] en [AD] ≅ [A'D']. Doe nu de volgende opgave.
Opgave 13: Voltooi het bewijs van stelling 8.1.
Stelling 8.2 : Een hoek die congruent is met een rechte hoek is zelf recht.
Ofwel: stel dat ∠BAC en ∠CAD een lineair paar vormen en ∠BAC ≅ ∠CAD; stel dat ∠B'A'C' en ∠C'A'D' een lineair paar vormen en ∠B'A'C' ≅ ∠BAC.
Dan ∠B'A'C' ≅ ∠C'A'D'.
Bewijs met stelling 8.1 volgt ∠C'A'D' ≅ ∠CAD, dus ∠C'A'D' ≅ ∠CAD ≅ ∠BAC ≅ ∠B'A'C'.
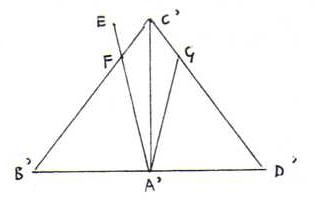
2) Stelling 8.3 : Alle rechte hoeken zijn congruent.
Ofwel: stel dat ∠BAC en ∠CAD een lineair paar vormen en congruent zijn; stel dat ∠B'A'C' en ∠C'A'D' een lineair paar vormen en congruent zijn. Dan ∠B'A'C' ≅ ∠BAC.
Bewijs: Kies B' en D' zo dat [A'B'] ≅ [A'D'].

Dan ΔA'B'C' ≅ ΔA'D'C' (zhz), dus ∠B' ≅ ∠D'.
Kies E aan dezelfde kant van lijn ←A'D'→ als C' zo dat ∠B'A'E ≅ ∠BAC.
We moeten bewijzen dat de stralen [A'E→ en [A'C'→ samenvallen.
Stel niet, zeg E ligt binnen ∠B'A'C'.
Laat straal [A'E→ segment [B'C'] snijden in F (kruisstelling).
Kies G in segment [D'C'] zo dat [D'G] ≅ [B'F].
Dan ΔA'B'F ≅ ΔA'D'G (zhz), dus ∠B'A'F ≅ ∠D'A'G.
Volgens stelling 8.1 is ΔD'A'E ≅ ΔCAD, dus ∠D'A'E ≅ ∠CAD ≅ ∠BAC ≅ ∠B'A'E ≅ ∠D'A'G.
Maar E en G liggen aan dezelfde kant van ←A'D'→ als C' en aan verschillende kanten van ←A'C'→. Tegenspraak met opgave 8 2).
3) Stelling 8.4 : Door een punt P op een lijn l gaat precies één lijn loodrecht op l.
Bewijs: Er bestaan rechte hoeken (vgl stelling 6.6). Zij Q een ander punt van l. Er bestaat een punt R zodat ∠QPR congruent is met een rechte hoek (zie opgave 8 2)). Dus ∠QPR is recht (stelling 8.2). Als er nog een ander punt R' is zodat ∠QPR' recht is, dan ∠QPR ≅ ∠QPR' (stelling 8.3). Dus de stralen [PR→ en [PR'→ vallen samen (opgave 8 2)).
4) Wat kan als vervanging van de driehoeksongelijkheid dienen? Men kan wel 'segmenten optellen' als ze in elkaars verlengde liggen, maar als dat niet het geval is ...?

Men kan equivalentieklassen van congruente segmenten beschouwen en een optelling definiëren in de verzameling der congruentieklassen.
Maar dat is ingewikkeld, en laten we verder achterwege.
Men kan afstand en hoekmaat ook invoeren door aan bovengenoemde axioma's voor een synthetische opbouw de volgende 'axioma's van continuïteit' toe te voegen:
Axioma van Archimedes:
Stel A en B liggen op l; laat A1, A2, ... een rij punten op l zijn zo dat voor alle k geldt A-Ak-Ak+1 en [AA1] ≅
[AkAk+1]. Dan bestaat n zo dat A-B-An.
Axioma der geneste intervallen:
Stel A en B liggen op l; laat A1, A2, ... en B1, B2, ... twee rijen punten op l zijn zo dat voor alle k geldt
A-Ak-Ak+1-Bk+1-Bk-B; stel dat verder geen punten C en D bestaan zo dat voor alle k geldt A-Ak-C-D-Bk-B;
dan is er precies één punt X zo dat voor alle k geldt A-Ak-X-Bk-B.
OPGAVE 14: Laat g, h, k, k1, k2, ... stralen met hetzelfde eindpunt zijn; stel dat k binnen ∠(g,h) ligt, k1 tweedeler van ∠(g,h) is, en, voor alle m,
km+1 tweedeler van ∠(km,h); bewijs dat n bestaat zo dat kn binnen ∠(k,h) ligt.
We hebben nu alle axioma's voor de 'absolute meetkunde' (de meetkunde van Euclides-Hilbert zonder het parallellenpostulaat).