NON-EUCLIDEAN GEOMETRY
for the interested layman
((Whatever is standing between double brackets, you may skip when you read this for the first time.))
1) Disturbances in our view on the world
In the third century before Christ, the Greek mathematician Euclid was working in the famous hellenistic library of Alexandria, at the mouth of the river Nile. His masterpiece, the Elements,
has stayed the standard for plane geometry until the twentieth century. It has been deduced from some definitions and axioms using only the strict rules of Aristotle's logic.
However, although his method has made a huge impression, it doesn't meet modern demands.
Euclid's definition of a point, 'that which has no part', is to some extent understandable. But a straight line is, according to Euclid, 'lying evenly with its points on itself', and
we can't make head or tail of it.
The seventeenth century French philosopher Pascal said we shouldn't try and define something everybody has a clear idea of. But it remains to be seen whether somebody has a clear idea of what a
straight line is. According to Plato, we know beforehand what a straight line is, because he thinks the concept is innate. On the contrary, according to Aristotle, we form the concept 'straight line' by
abstraction, after having seen many more or less rectilinear objects. But nobody ever saw a perfectly straight line. Indeed, every ray of light is turned aside, be it ever so little, in the field of gravity
it's propagating in. In fact, nowadays, mathematicians don't try to define the concept 'straight line' any more. This does give geometrists the freedom to substitute their own concept for it.
Euclid also formulated some ten axioms for his (euclidean) plane geometry. For instance: there exists exactly one straight line that goes through two given points. Or, another example:
the whole is greater than the part. But among his axioms, there's one that mathematicians always considered an intruder (because it's a bit more complicate than the other ones).
That's the parallel postulate, which reads in a later formulation:
Suppose we have a straight line BC and a point A outside it. Then there exists exactly one straight line that's going through A and parallel to BC (see the picture).
Using this parallel postulate, we can prove that in any triangle the sum of the angles is 180 degrees (to see this, look again at the picture).
Throughout the centuries, mathematicians tried to deduce the parallel postulate from the other axioms. As soon as they had success, they could omit it as an axiom for Euclid's geometry.
The Italian Jesuit Saccheri has been trying it about 1700 with much discipline. More than a century later on, the French mathematician Legendre died while happily thinking his endeavours had been successful.
However, in his proof he had used something that was equivalent to the very parallel postulate he wished to prove.
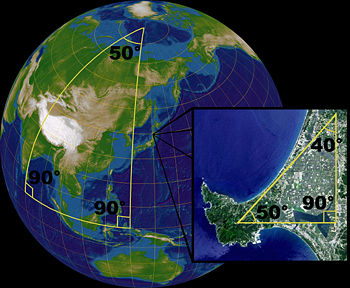
The famous German mathematician Carl Friedrich Gausz suspected, about 1850, that the parallel postulate doesn't even hold in our cosmos, because our cosmos is non-euclidean. To prove that, he measured the
angles of the triangle formed by three mountain tops, hoping they wouldn't sum up to 180 degrees. But the deviation he found was within the measuring fault.
If he had been able to measure from three stars instead of three mountain tops, the sum of the angles may have turned out to be not equal to 180 degrees, because our cosmos is probably
'curved' and non-euclidean indeed.
Gausz didn't want to noise his suspicion abroad, because he was afraid people would denounce him like Galilei.
2) Non-euclidean geometries
In the nineteenth century, geometrists like Lobachevsky and Riemann developed geometrical systems, starting from Euclid's, by substituting a different axiom for the parallel postulate.
By substituting their own concept of 'straight line' for the one that Euclid intended, geometrists also found models for these new geometrical systems, as we will show beneath.
In these models, the parallel postulate doesn't hold, but the other axioms of Euclid do.
Hence they proved at once it's impossible to deduce the parallel postulate from the other axioms, so the endeavours of Saccheri and Legendre couldn't but fail. And this shows again how clever Euclid was,
because he already saw he needed the parallel postulate as an independent axiom.
Riemann developed a system of 'plane' geometry on the surface of a sphere. The surface of a sphere isn't really flat, but it appears so when seen from very near. Examples of 'straight lines' are the
meridians and the equator. These 'straight lines' aren't really straight, but they seem straight when seen from very near. We saw above that a ray of light doesn't follow a straight line, either.
The 'straight lines' of Riemann's model are geodesics, that is to say: the shortest path over the sphere between two points on the sphere is such a 'straight line'.
((To be exact: a 'straight line' of this geometry is (by definition) a 'great circle' on the sphere, that is a circle on the surface of the sphere that lies in a plane through the centre of the sphere.))
Two 'straight lines' that seem to be parallel, for example the meridians at an eastern longitude of three and four degrees respectively, always intersect (in the two poles).
This is a model of an elliptic geometry. Instead of the parallel postulate we have the postulate that through a point A outside BC there goes no 'straight line' that is parallel to BC,
or with other words: any two 'straight lines' intersect (even in two points), so there's no parallelism. In the picture beneath you can see three 'straight lines' forming a triangle whereof the sum
of the angles isn't 180 degrees, but 230 degrees. In the inset you can see that in 'small' parts of the surface of the sphere the angles do sum up to (a bit more than) 180 degrees. In elliptic geometry,
the angle sum is greater than 180 degrees in every triangle.
The French geometrist Poincaré developed a system of plane geometry within a circular disc. See the picture made by the famous artist Escher: the (shown) 'straight lines' are the white lines over
the backs of the little fishes.
Here, too, the designer of the system substituted his own concept of 'straight line': the 'straight lines' aren't really straight, but they seem straight when seen from very near.
((To be exact: a 'straight line' of this geometry is either a (real) straight line through the centre of the circular disc, as far as it's lying within the circular disc, or part of a circle that
is perpendicular to the edge of the circular disc, namely the part that's lying within the circular disc. The 'straight lines' are the geodesics with respect to the metric that Poincaré imposed on
his model.))
Can you discover a 'straight line' BC and a point A outside BC and three straight lines through A that don't intersect BC, so are 'parallel' to BC?
Do you also see the little triangles formed by white lines over the backs of three little fishes that are lying close together and have distinct colours? And do you see the angle sum is less than 180
degrees?
This is a model of an hyperbolic geometry. Instead of the parallel postulate we have the postulate that through a point A outside BC there goes more than one 'straight line' that is parallel
to BC. In hyperbolic geometry,
the angle sum is smaller than 180 degrees in every triangle.

3) A bit of speculation
It seems our cosmos is still expanding as a consequence of the big bang. This appears from the fact that the Doppler effect makes stars show a greater redshift in the colour spectrum as they
are farther away from us.
Until some forty years ago, astronomers thought their calculations would best fit the observations if they used an elliptic (closed) model for the cosmos. In this model, which Einstein used for his general
theory of relativity, the expansion of the cosmos will eventually stop, and turn into shrinking.
Einstein considered our cosmos a sort of dynamical super-sphere in space-time. The cosmos is 'positively curved' (see the picture which gives a two-dimensional equivalent).
If we would propagate with the speed of light over this super-sphere, following a 'straight line' ((that is the sequence of space-time events of a free-falling body)),
then we would return at our starting point after some thirty billion years.
Nowadays, other astronomers prefer to use a hyperbolic (open) model, in which the cosmos is 'negatively curved'. According to them, the expansion of the cosmos will never stop. The question is whether the
total amount of mass in the cosmos is greater or smaller than some critical value.
Finally, the euclidean (flat) model is making a remarkable come-back as a consequence of new evidence, indicating that the total amount of mass might be exactly equal to the critical value.

If there has been a big bang, then this big bang must have been caused. But the cosmos is asking for a cause anyway.
If you believe in God, you may imagine He maintains, as long as He thinks fit, the whole space-time with big bang and history and (if appropriate) big crunch.
Literature
Wikipedia with search words 'non-euclidean geometry' and 'big bang'.
Euclid's Elements (very extensive, and not easy)
Niet-Euclidische Meetkunde, prof dr G Verriest, KCT Streven 1948 (in Dutch)
The Geometry of the Universe
The Ontology and Cosmology of Non-Euclidean Geometry