11248 Let n be a positive integer, and let f be a continuous real-valued function on [0,1] with the property that INT(x from 0 to 1: xkf(x) dx) = 1 for k=0,1,...,n-1. Prove that INT(x from 0 to 1: f(x)2 dx) is at least n2.
Solution:
Using that for any reals c0, c1, ... , cn-1, INT(x from 0 to 1: (f(x)-SUM(k from 0 to n-1: ckxk))2 dx) is at least 0, we derive:
INT(x from 0 to 1: f(x)2 dx) is at least
c0(2 - c0/1 - c1/2 - c2/3 - c3/4 - ... - cn-1/n) +
c1(2 - c0/2 - c1/3 - c2/4 - c3/5 - ... - cn-1/(n+1)) +
c2(2 - c0/3 - c1/4 - c2/5 - c3/6 - ... - cn-1/(n+2)) +
... +
cn-1(2-c0/n-c1/(n+1)-c2/(n+2)-c3/(n+3)-...-cn-1/(2n-1)).
To maximize this sum, we set the partial derivatives equal to 0. This amounts to setting the n expressions between brackets
equal to 1.
We calculate c0, c1, ... , cn-1, using the inverse of the well-known matrix
with coefficients 1/(i+j-1). Then the sum turns out to be equal to n2.
11249 A node-labeled rooted tree is a tree such that any parent with label p has p+1 children, labeled 1,2,..,p+1, and such that the root vertex (generation 0) has label 1. Find the population of generation n.
Solution:
Let g(k)(m) be the number of labels m of generation k.
Initialize
g(k)(0):=0 for all k, g(0)(1):=1. Furthermore use the following recurrence relation:
For k=1,2,3,... successively, for m from 1 to k+1, calculate g(k)(m):=SUM(p from m-1 to k: g(k-1)(p)).
Clearly the population g(n)total of generation n is g(n+1)(1)=g(n+1)(2).
I did the calculations for k from 1 to 10, using a triangular matrix schedule (g(k)(m)). I found
g(n)total=1,2,5,14,42,132,429,1430,4862,16800 for n=1,2,..,10.
Furthermore, looking at the matrix elements, I discovered an easier calculation scheme:
Initialize g(k)(0):=0 and g(k)(k+1):=1 for k=0,1,2,3,...
For k=1,2,3,... successively, for m:=k downto 1, calculate
g(k)(m):=g(k)(m+1)+g(k-1)(m-1).
This reminds us of the Pascal triangle. But why should we express the results
g(n)total in binomial coefficients, if our triangle is as easy as Pascal's?
11250 Show that if n is a positive integer and x1, x2, ... xn are nonnegative
real numbers that sum to 1, then
(SUM j: j from 1 to n: sqrt(xj))*(SUM k: k from 1 to n: 1/(1+sqrt(1+2xk)) is at most
n2/(sqrt(n)+sqrt(n+2)).
Partial solution:
Since the right hand side of the inequality is increasing as a function of n, and the case n=1 is trivial, we may assume without loss of generality that all xi are positive and smaller than 1. Therefore the maximum of the left hand side is attained in a point of Lagrange. With our restriction x1+x2+...+xn=1, this means that all partial derivatives must be equal. We want to deduce that, then, all xi must be equal. Then the maximum is attained for xi=1/n (all i); thus we get the right hand side as maximum for the left hand side.
Suppose that among the xi there exist x and y with x smaller than y.
We calculate the partial derivatives, and use they must be equal. Then we get:
(SUM k: k from 1 to n: 1/(1+sqrt(1+2xk))*(1/(2*sqrt(x))-1/(2*sqrt(y))) =
(SUM j: j from 1 to n: sqrt(xj))*(1/((sqrt(1+2x)*(1+sqrt(1+2x))2)-1/((sqrt(1+2y)*(1+sqrt(1+2y))2)).
Somehow, this must lead us to a contradiction.
11251 Let a,b and c be positive real numbers, two of which are less than or equal to 1, satisfying ab+ac+bc=3.
Show that
1/(a+b)2+1/(a+c)2+1/(b+c)2-3/4 is at least 3(a-1)(b-1)(c-1)/(2(a+b)(a+c)(b+c)).
Practical solution:
This amounts to checking whether 4(a2+3)2(b2+3)2+ 4(a+b)4(b2+3)2+4(a+b)4(a2+3)2 is at least 3(a+b)2(a2+3)(b2+3)(15+5a2+5b2+8ab-8a-8b-a2b2) for a and b between 0 and 1 (inclusive). I did this with Maple.
11252 Let n be an integer greater than 2, and let a1, a2, ... , an be positive
numbers.
Let S=SUM(i from 1 to n: ai ). Let bi=S-ai and let
S' =SUM(i from 1 to n: bi ). Show that
PRODUCT(i from 1 to n: ai )/PRODUCT(i from 1 to n: S-ai )
is less than or equal to PRODUCT(i from 1 to n: bi )/PRODUCT(i from 1 to n: S'-bi ).
Provisional solution:
Since S'= (n-1)S and S'-bi=(n-2)S+ai, the inequality is equivalent to
PRODUCT(i from 1 to n: ai )*PRODUCT(i from 1 to n: (n-2)S+ai ) is less than or equal to
PRODUCT(i from 1 to n: (S-ai )*PRODUCT(i from 1 to n: (S-ai ), or
PRODUCT(i from 1 to n: ai2-2*S*ai+n*aiS ) is less than or equal to
PRODUCT(i from 1 to n: ai2-2*S*ai+S2 ).
Now the sum of the factors at the left hand side of this last inequality is the same as the sum of the factors at the right hand side,
but the factors at the left hand side have a greater variation. It is wellknown that in such a case the product at the left
hand side is less than or equal to the product at the right hand side.
11253 Let n be a positive integer and A an n by n matrix with all entries ai,j positive. Let P be the permanent of A. Prove that P is at least n! times (PRODUCT(i,j from 1 to n: ai,j))1/n.
Solution:
By definition, P is equal to (SUM s: s permutation of {1,2,..,n}: as(1),1as(2),2...as(n),n).
By the arithmetic-geometric mean inequality, this is at least n! times (PRODUCT: s permutation of {1,2,..,n}:
as(1),1as(2),2...as(n),n))1/(n!).
The right hand side is equal to n! times (PRODUCT(i,j from 1 to n: ai,j))((n-1)!)/(n!).
11254 For a prime p greater than 3, let Sp be the set of positive integers less than (p-1)/2 and relative prime to p-1. Characterize the primes p for which there exists a primitive root g modulo p such that the product of ga, taken over all a in Sp, is also a primitive root modulo p.
Partial solution:
Any root of unity modulo p is primitive iff it has order p-1, and any power of a primitive
root is also primitive iff the exponent is relative prime to p-1. Since a primitive root of unity g always exists, p
satisfies the demand iff the sum of the elements of Sp is relative prime to p-1.
The primes p between 3 and 30 which satisfy the demand are the following: 5,7,19,23.
I searched the internet and the book of Hardy and Wright for a formula that gives the sum of the elements of Sp,
but in vain.
11256 For complex numbers a,b and c, let f(x)=max(Re(a*eix),Re(b*eix,Re(c*eix)).
Find INT(x from 0 to 2*pi: f(x) dx).
Solution:
Let a=a1+ia2 (a1,a2 real), and likewise for b and c.
Re(a*eix)=A=a1cos(x)-a2sin(x), and likewise for b and c.
Without loss of generality we assume a2 is at least b2, and b2 at least c2.
We find: A is larger than B iff ((x lies between -pi/2 and pi/2, and tan(x) is smaller than
(a1-b1)/(a2-b2)) or (x lies between pi/2 and 3*pi/2, and tan(x) is greater than
(a1-b1)/(a2-b2))).
Let at(a,b)=arctan((a1-b1)/(a2-b2)), and likewise at(a,c) and at(b,c).
We find: A is larger than B iff ((x lies modulo 2*pi between -pi/2 and at(a,b)) or (x lies modulo 2*pi between pi+at(a,b)
and 3*pi/2)).
Now henceforth we assume, for instance, that at(a,c) lies between at(a,b) and at(b,c) (other cases are similar).
Then max(A,B,C)=B for x modulo 2*pi lying between
at(a,b) and at(b,c), max(A,B,C)=C for x modulo 2*pi lying between at(b,c) and pi+at(a,c), max(A,B,C)=A for x modulo 2*pi
lying between pi+at(a,c) and 2*pi+at(a,b).
So INT(x from 0 to 2*pi: f(x) dx) = INT(x from at(a,b) to at(b,c): B dx) + INT(x from at(b,c) to pi+at(a,c): C dx) +
INT(x from pi+at(a,c) to 2*pi+at(a,b): A dx).
If x=at(b,c) then
sin(x)=(b1-c1)/sqrt((b1-c1)2+(b2-c2)2) =
(b1-c1))/sqrt(b,c), and cos(x)=(b2-c2)/sqrt(b,c), etc.
So INT(x from at(a,b) to at(b,c): B dx) = [b1sin(x)+b2cos(x)] (x in at(b,c) minus x in at(a,b)) =
(b1(b1-c1)+b2(b2-c2))/sqrt(b,c) -
(b1(a1-b1)+b2(a2-b2))/sqrt(a,b).
Likewise we find: INT(x from at(b,c) to pi+at(a,c): C dx) =
-(c1(a1-c1)+c2(a2-c2))/sqrt(a,c) -
(c1(b1-c1)+c2(b2-c2))/sqrt(b,c); and:
INT(x from pi+at(a,c) to 2*pi+at(a,b) : A dx) = (a1(a1-b1)+a2(a2-b2))/sqrt(a,b)
+ (a1(a1-c1)+a2(a2-c2))/sqrt(a,c).
These terms sum up to sqrt(a,b)+sqrt(b,c)+sqrt(c,a), this is the circumference of triangle ABC.
11261 A triangle of area 1 has vertices A1, A2 and A3. The sides
A2A3, A3A1, A1A2 subtend angles of measure
alpha1, alpha2, alpha3, respectively, at an internal point P. The triangle has
angles at A1, A2, A3 of measure a1, a2, a3,
respectively. The extensions of A1P, A2P, A3P to their opposite sides meet those sides
at B1, B2, B3 respectively.
Express the area of triangle B1B2B3 in alpha1, alpha2, alpha3,
a1, a2 and a3.
Partial solution:
Give coordinates P(0,0), A2(r,0), A3(s*cos(alpha1),s*sin(alpha1)),
A1(t*cos(alpha3),-t*sin(alpha3), and
B2(-u,0),
B3(-v*cos(alpha1),-v*sin(alpha1)),
B1(-w*cos(alpha3),w*sin(alpha3)).
Using that B2 lies on A1A3 we get
u=s*t*sin(alpha2)/(s*sin(alpha1)+t*sin(alpha3)). Likewise:
v=r*t*sin(alpha3)/(r*sin(alpha1)+t*sin(alpha2)),
w=s*r*sin(alpha1)/(s*sin(alpha2)+r*sin(alpha3)).
So we can express the side lengths B2B3, B3B1, B1B2
in r,s,t and alpha1, alpha2, alpha3.
Furthermore, using A1A2*A1A3*sin(a1)/2 = 1, etc, we find
A1A2 = sqrt((2*sin(a3)/(sin(a1)*sin(a2))), etc.
So, using Heron's formula for the area of triangle B1B2B3, we can now reach our
aim if we can express r,s,t in the angles
alpha1,alpha2,alpha3 and the side lengths
A2A3, A3A1, A1A2.
This last task can be done, at least in principle, by using
A1A22 = r2+t2-2*r*t*cos(alpha3),
A2A32 = r2+s2-2*r*s*cos(alpha1),
A1A32 = s2+t2-2*s*t*cos(alpha2).
Remark: If we use the formula for the area of a Cevian triangle with given trilinear coordinates, we
get
2*rst*sin(alpha1)*sin(alpha2)*sin(alpha3)/((r*sin(alpha1)+t*sin(alpha2))*
(s*sin(alpha1)+t*sin(alpha3))*(s*sin(alpha2)+r*sin(alpha3))).
But then, again, we still have to express r,s,t in the angles
alpha1,alpha2,alpha3 and the side lengths
A2A3, A3A1, A1A2.
11309 Let c and d be real numbers with sqrt(c2+d2) smaller than pi/2. Prove that cos(c*sin(x)) is greater than sin(d*cos(x)) for all real x.
Solution:
Note that c=r*cos(e) and d=r*sin(e) for some real e and r from [0,pi/2).
We distinguish cases a): c*sin(x) positive, b): c*sin(x) nonpositive.
In case a) we observe that cos(c*sin(x)) = sin(pi/2-c*sin(x)) and sin is strictly ascending on (-pi/2,pi/2);
since d*cos(x) is greater than -pi/2, pi/2-c*sin(x) smaller than pi/2, and
c*sin(x)+d*cos(x) = r*sin(e+x) smaller than pi/2, so pi/2-c*sin(x) greater than d*cos(x), we find that the inequality in the problem is true.
In case b) we observe that sin(d*cos(x)) = cos(pi/2-d*cos(x)) and cos(c*sin(x)) = cos(-c*sin(x)) and cos is strictly descending on [0,pi);
since -c*sin(x) is greater than or equal to 0, pi/2-d*cos(x) smaller than pi, and
-c*sin(x)+d*cos(x) = r*sin(e-x) smaller than pi/2, so pi/2-d*cos(x) greater than -c*sin(x), we find that the inequality in the problem is true.
11315 Define f on the positive integers by letting f(n)=PRODUCT(k from 1 to r: akpk) when n has prime factrorization PRODUCT(k from 1 to r: pkak), with the empty product yielding f(1)=1. Prove that for all n the sequence n, f(n), f(f(n)), ... , is eventually periodic, with period at most 2.
Partial solution:
The sequence becomes periodic, with period 1 or 2, as soon as we get a term whose prime factorization has only exponents that are prime and distinct.
But this will always happen at some moment, because the sequence SUM(k from 1 to r: ak+pk), derived from the prime factorizations of the terms, is mostly decreasing until it happens.
11325 Let P be a point within a triangle ABC. Let the lines AP, BP and CP intersect the sides BC, CA and AB at L, M, N respectively. Show that AP*BP*CP is at least 8*LP*MP*NP, with equality iff P is the centroid of ABC.
Solution:
Give coordinates P(0,0), A(-a,0), L(1,0) and, for some t with sin(t) not equal to 0, B(1+b*cos(t),b*sin(t)), C(1-c*cos(t),-c*sin(t)) (a,b,c positive).
We calculate the coordinates of M and N and find, besides AP/LP = a, the ratios BP/MP = (b+c+ac)/(ab) and CP/NP = (b+c+ab)/ac.
Hence we have to prove that for positive a,b,c holds: (b+c+ac)(b+c+ab) - 8abc (= f) is at least 0, with equality iff the three ratios are equal to 2.
We may write f/(bc) = (a+(s-8)/2)2 + s-(s-8)2/4 with s=(b+c)2/(bc).
Now s-(s-8)2/4 is positive for s in (4,16), and, since a is positive, for s at least 16 we find that f is positive.
Furthermore, s is at least 4 with equality iff b=c. If s=4 then f=(a-2)2.
Hence, for positive a,b,c we find: f is at least 0 with equality iff (b=c and a=2).
Finally, it is straightforward to show that the three ratios are equal to 2 iff (b=c and a=2).
11328 Let ABCD be a convex quadrilateral. Let P be a point outside ABCD such that angle APB is a right angle and P is equidistant from A and B. Let points Q, R and S be given by the same conditions with respect to the other three edges of ABCD. Let J, K, L and M be the midpoints of PQ, QR, RS and SP, respectively. Prove that JKLM is a square.
Solution:
Give coordinates A(0,0), B(1,0), C(c1,c2), D(d1,d2) with c2 and d2 positive and c1 greater than d1.
Then we find P(1/2,-1/2), Q(1/2+c1/2+c2/2,1/2-c1/2+c2/2), R(c1/2-c2/2+d1/2+d2/2,c1/2+c2/2-d1/2+d2/2),
S(d1/2-d2/2,d1/2+d2/2)
and hence J(1/2+c1/4+c2/4,-c1/4+c2/4), K(1/4+c1/2+d1/4+d2/4,
1/4+c2/2-d1/4+d2/4), L(c1/4-c2/4+d1/2,c1/4+c2/4+d2/2),
M(1/4+d1/4-d2/4,-1/4+d1/4+d2/4).
Now it's straightforward to show that the vectors JK and KL are perpendicular, and likewise KL and LM, LM and MJ, MJ and JK, and that the four lengths
|JK|, |KL|, |LM| and |MJ| are equal.
11330 For a triangle with semiperimeter s, inradius r, circumradius R, and heigths ha, hb, hc, show that
ha+hb+hc - 9r is at least 2s*√(2r/R) -6r*√3.
Partial solution:
As several times before, we use:
1) area D = ab*sin(γ)/2 = bc*sin(α)/2 = ac*sin(β)/2 = (1/2)*(abc)2/3(sin(α)*sin(β)*sin(γ))1/3;
2) r = D/s = 2D/(a+b+c), R = abc/(4D);
3) ha=c*sin(β), hb=a*sin(γ), hc=b*sin(α);
4) a/sin(α) = b/sin(β) = c/sin(γ) = h.
Then we find, again, that the proposed inequality is equivalent to a goniometric inequality that we may check using Pascal. This time it reads:
(α, β, γ positive and summing up to π, and)
(sin(α)+sin(β)+sin(γ))(sin(α)*sin(β)+sin(α)*sin(γ)+sin(β)*sin(γ)) ≥ 2√(sin(α)+sin(β)+sin(γ))*√(sin(α)*sin(β)*sin(γ))*(sin(α)+sin(β)+sin(γ)) + (9-6*√3)*sin(α)*sin(β)*sin(γ).
{The Pascal program includes the following central part:
for k:=0 to 10000 do for m:=k to (15000 - (k div 2)) do begin a:=k*pi/30000; b:=m*pi/30000; c:=pi-a-b; f:= .... ; if not (f ≥ 0) then writeline(k:6,m:6) end}
We have equality if α = β = γ = π/3.
11333 Show that PRODUCT(n from 2 to inf: ((n2-1)/n2)2(n2-1)((n+1)/(n-1))n) = π.
Solution:
PRODUCT(n from 2 to N: ((n2-1)/n2)2(n2-1)((n+1)/(n-1))n) =
2*32*42*52*..*N2*(N/(N+1)2)*(N+1)2N2+N/N2N2+3N.
We can replace (N+1)2N2+N/N2N2+3N by (e2N/N2N) asymptotically.
Furthermore, we can replace (N/(N+1)2) by 1/N asymptotically.
Hence the infinite product is LIM(N to inf: (N!)2(e2N/N2N)/(2N)). According to Stirling, this becomes π.
11337 Suppose in triangle ABC we have opposite sides of length a,b,c respectively, with a≤b≤c. Let wa and wb be the lengths of the bisectors of the angles A and B respectively. Show that a+wa ≤ b+wb.
Partial solution:
Without loss of generality we may assume: c=1; A(0,0), B(1,0), C(b*cos(α),b*sin(α)).
We find wa=2b*cos(α/2)/(1+b), wb=2a*cos(β/2)/(1+a).
So we have to prove: 2b(1+a)cos(α/2)-2a(1+b)cos(β/2) ≤ (b-a)(1+a)(1+b).
Now, according to the sine rule a/sin(α)=b/sin(β)= 1/sin(α+β). So the inequality becomes:
sin(α+β)(2sin(β)(sin(α+β)+sin(α))cos(α/2)-2sin(α)(sin(α+β)+sin(β))cos(β/2)) ≤ (sin(β)-sin(α))(sin(α+β)+sin(α))(sin(α+β)+sin(β)) for 0≤α≤β≤π-α-β.
This can be checked with Pascal.
11345 Find all nondecreasing functions f from ℜ to ℜ such that f(x+f(y)) = f(f(x)) + f(y) for all x and y.
Solution:
Suppose f(0)=A. Substituting x=y=0 yields f(A)=f(A)+A, so A=0. So f(0)=0.
Then substituting y=0 yields f(x)=f(f(x)) for all x.
So if f(x)=B then f(B)=B. So for any B in the range of f we have f(B)=B.
Furthermore, we find f(x+f(y)) = f(x) + f(y) for all x and y. Hence, if B and C belong to the range of f then f(x+C) = B+C for all x with f(x)=B.
Now suppose f(y)=C. Substituting x=-C yields 0 = f(0) = f(-C+C) = f(-C) + C. So f(-C) = -C. Hence, if C belongs to the range of f, then so does -C.
If B and C belong to the range of f, then f(B)=B and f(C)=C and f(B+C) = B+C, so B+C belongs to the range of f.
Conclusions:
1) The range f(ℜ) of f is a subgroup of (ℜ,+).
2) If f(ℜ) has a smallest positive element E then, for all D ∈ f(ℜ), f-1(D) is a half open interval of length E containing D, obtained by translating
f-1(0) a distance k times E for some integer k; so f is a kind of step function.
3) If f(ℜ) has no smallest positive element E then either f(x)=0 for all x or f(x)=x for all x.
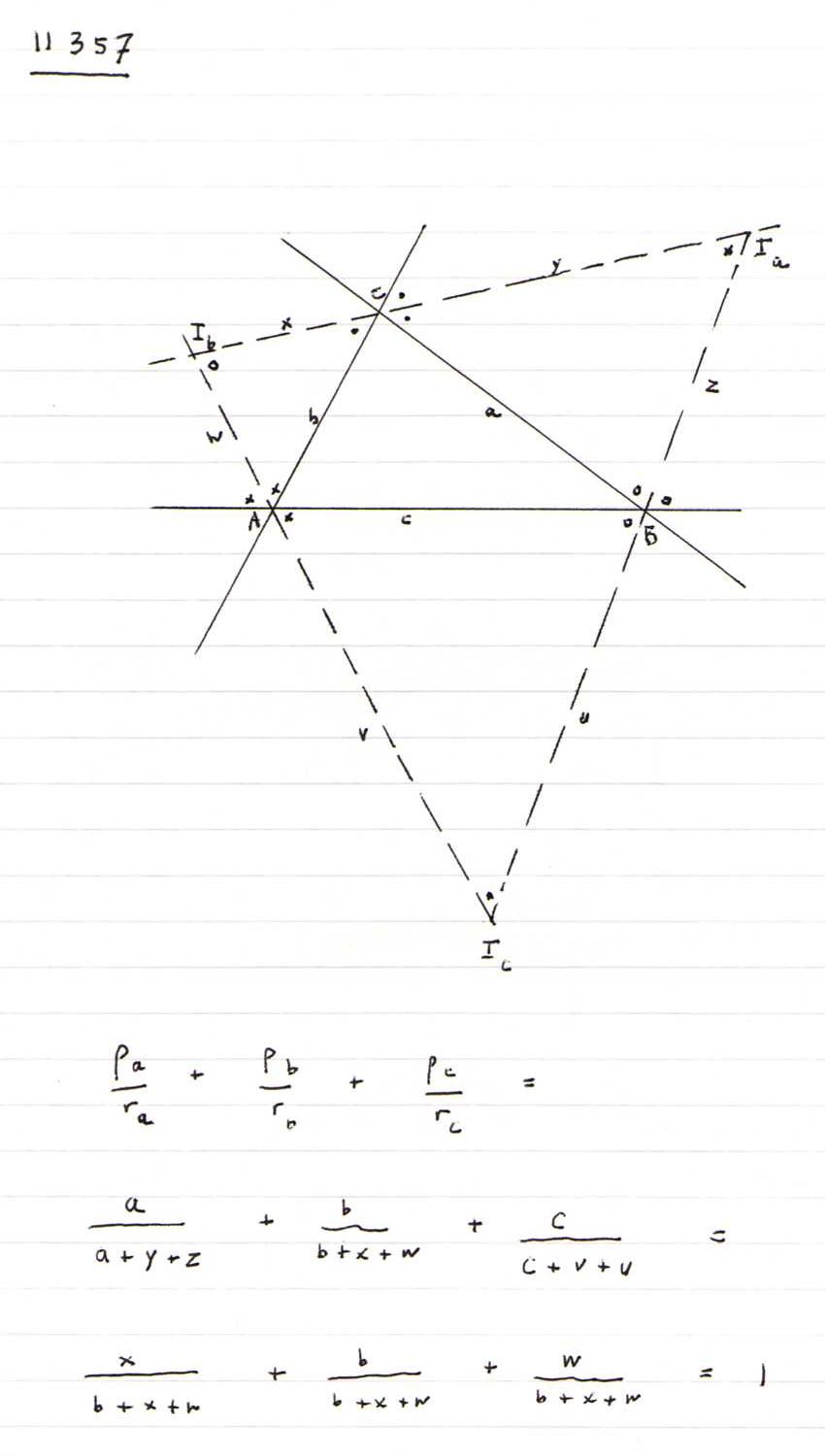
11357 Let Ia , Ib , Ic and ra , rb , rc be respectively the excenters and exradii of the triangle ABC.
If ρa , ρb , ρc are the inradii of triangles IaBC , IbCA , IcAB , show that
ρa /ra + ρb /rb + ρc /rc = 1.
Solution:
The picture below explains everything.

11397 Let a,b,c,x,y,z be positive numbers such that a+b+c = x+y+z and abc = xyz. Show that if max{a,b,c} ≥ max{x,y,z}, then min{a,b,c} ≥ min{x,y,z}.
Solution:
Suppose f = U3 + pU2 + qU + s = (U-a)(U-b)(U-c) and g = U3 + pU2 + rU + s = (U-x)(U-y)(U-z),
where a ≥ b ≥ c > 0 and x ≥ y ≥ z > 0.
Then g - f = (r-q)U = tU.
If a ≥ x then t ≥ 0 and we have the following picture:
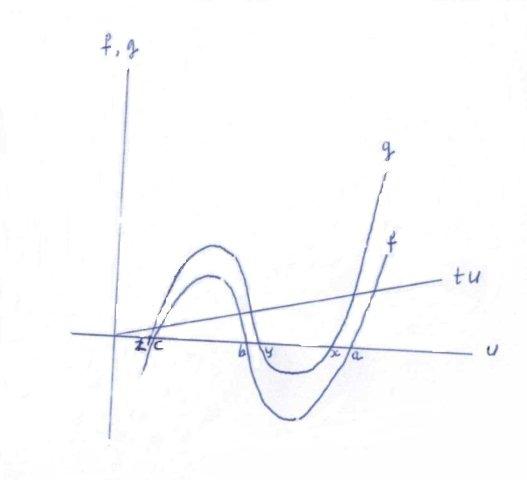
So c ≥ z.
11398 Suppose that acute triangle ABC has its middle-sized angle at A. Suppose further that the incenter I is equidistant from the circumcenter O and the orthocenter H.
Show that angle A has measure 60 degrees and that the circumradius of IBC is the same as that of ABC.
Partial solution:
From Wolfram we learn: if D is the area of the triangle and R = abc/(4D) is the circumradius and r = 2D/(a+b+c) is the inradius, then
IO = √(R(R-2r)), IH = √(2r2 + 4R2 -(a2+b2+c2)/2).
Now let h := a/sin(α) = b/sin(β) = c/sin(γ). Then D = ab sin(γ)/2 = h2sin(α)sin(β)sin(γ)/2.
We deduce R = h/2 and r = h*sin(α)sin(β)sin(γ)/(sin(α)+sin(β)+sin(γ)).
So IO = IH is equivalent to 1/4 - sin(α)sin(β)sin(γ)/(sin(α)+sin(β)+sin(γ)) = 2*(sin(α)sin(β)sin(γ)/(sin(α)+sin(β)+sin(γ)))2 + 1
- (sin2(α) + sin2(β) + sin2(γ))/2.
With a Pascal program we seek all solutions of this last equation under the restraint α+β+γ = 180. We find: α=60, β and γ arbitrary such that β+γ
= 120.
If α = 60 then the angle at I in triangle IBC is 120. The circumradius of ΔABC is h/2 = a/(2*sin(60)), and the circumradius of ΔIBC is a/(2*sin(120)). So these two circumradii are always equal if α = 60.
11402 Let f:[0,1] → [0,∞) be a continuous function such that f(0) = f(1) = 0 and f(x) is positive for x ∈ (0,1).
Show that there exists a square with two vertices in the interval (0,1) on the x-axis and the two other vertices on the graph of f.
Partial solution:
Here is the solution when f is increasing at the beginning of (0,1) and decreasing at the end.
Let c ∈ (0,1] be maximal such that f(x) is at most 1-x for all x ∈ [0,c].
Let g(x) := f(x+f(x)) - f(x).
Then g is continuous on [0,c].
Let s be maximal such that f is increasing on [0,s] and let t ∈ [0,s] be maximal such that f(x) is at most s-x on [0,t].
Then, for every δ ∈ (0,t), g(δ) is positive.
Analoguously, if c=1, there exists a positive ε (smaller than 1-t) such that g(1-ε) is negative (because f is decreasing on [u,1] for some u ∈ [s,1]).
Again, if c is smaller than 1, then for ε := 1-c (positive and smaller than 1-t) we find g(1-ε) is negative (because g(1-ε) = g(c) = f(c+f(c))-f(c) = f(1)-f(c) = -f(c)).
Now, since g(δ) is positive and g(1-ε) negative, there exists an u ∈ (δ,1-ε) such that g(u) = 0.
Since f(u+f(u)) = f(u), we find a square as required.
11404 Any three non-concurrent cevians of a triangle create a subtriangle. Identify the set of non-concurrent cevians which create a subtriangle whose incenter coincides with the incenter of the primary triangle (a cevian is a line segment joining a vertex to an interior point of the opposite edge.)
Partial solution:
If we use coordinates such that the incenter is (0,0), and one of the sides of the primary triangle is y=-1, and the other two sides have direction coefficients m (positive) and n (negative), then the vertices have
coordinates
(-(√(m2+1)+1)/m,-1) , (-(√(n2+1)+1)/n,-1), and (U,V) =
((√(n2+1)-√(m2+1))/(m-n),(m(√(n2+1)-1)-n(√(m2+1)-1))/(m-n)).
Now if the cevians from these three vertices have direction coefficients (respectively) a ∈ (0,m), b ∈ (n,0) and c ∈ (n,m), then, because the distances from (0,0) to these three cevians
must be equal, we find two independent linear equalities that relate a,b,c to m,n (so there is a one-dimensional solution set for (a,b,c)). These inequalities read:
|((a/m)(1+√(m2+1))-1)/√(a2+1)| = |((b/n)(1+√(n2+1))-1)/√(b2+1)| = |(Uc-V)/√(c2+1)|.
If we use A:=|a|/√(a2+1), etc, and M:=(1+√(m2+1))/|m|, etc, then the one-dimensional solution set for (A,B,C) has direction vector (|U|/M,|U|/N,1).
In each of the cases, we readily find the full solution set.
11405 Let P be an interior point of a tetrahedron ABCD. When X is a vertex, let X' be the intersection of the opposite face with the line through X and P. Let XP denote the length of the line
segment from X to P.
(a) Show that PA.PB.PC.PD ≥ 81PA'.PB'.PC'.PD', with equality if and only if P is the centroid of ABCD.
(b) When X is a vertex, let X" be the foot of the perpendicular from P to the plane of the face opposite X. Show that PA.PB.PC.PD = 81PA".PB".PC".PD" if and only if the tetrahedron is regular and P is
its centroid.
Solution:
(a) Let D=O and, for any point X, denote the vector from O to X by x.
If P is an interior point of tetrahedron OABC, then p = xa + yb + zc for positive x,y,z whose sum is smaller than 1.
We readily calculate PA' = x/(1-x)PA, PB' = y/(1-y)PB, PC' = z/(1-z)PC, PO' = (1-x-y-z)/(x+y+z)PO.
So we have to find the minimum of ((1-x)/x)((1-y)/y)((1-z)/z)((x+y+z)/(1-x-y-z)) for x,y,z as above.
We calculate the partial derivatives and demand that they be zero, and find x(1-x) = y(1-y) = z(1-z) = (x+y+z)(1-x-y-z) and hence x=y=z=1/4.
(b) If the tetrahedron is regular and P is the centroid, then X"=X' for all vertices X, so the equality holds.
If the tetrahedron is not regular or P is not the centroid, then PX/PX" ≥ PX/PX' for all vertices X and PX/PX" > PX/PX' for at least one vertex X, so the equality does not hold.
Earlier solutions 1: click here .
Earlier solutions 2: click here .
Earlier solutions 3: click here .
Earlier solutions 4: click here .
More solutions: click here