11747 Determine all natural numbers n such that ⌊ n/k ⌋ divides n for 1 ≤ k ≤ n.
Similarly, determine all natural numbers n such that ⌈ n/k ⌉ divides n for 1 ≤ k ≤ n
Partial solution:
I ran a pascal program and think the following lists are complete: 1,2,3,4,6,8,12,24 and 1,2,4,6,12.
11748 Is there a sequence of positive real numbers a1 , a2 , a3 , ... such that Πk=1n ak < nn and Σk=1∞ ak converges?
First consideration:
If Πk=1n ak = nn, then ak = kk / (k-1)(k-1), and then 1/ak is comparable to 1/(e(k-1)) if k→∞.
So in this case Σk=1∞ ak does not converge.
If Πk=1n ak < nn, then ak must be even smaller than kk / (k-1)(k-1) for some k,
so at first sight it seems Σk=1∞ ak can't converge. But there's more room for many ak to be larger ...
11751 In a triangle with angles of radian measures A,B and C, prove that (csc(A)+csc(B)+csc(C))/2 ≥ 1/(sin(B)+sin(C)) + 1/(sin(C)+sin(A)) + 1/(sin(A)+sin(B)) with equality iff the triangle is equilateral.
Numerical solution:
I checked this with a pascal program for all A,B,C corresponding to an integer number of degrees: for a:=1 to 60 do for b:=a to 90 - (a div 2) do begin c:=180-a-b ...
11753 Let f be a continuous map from [0,1] to ℜ that is differentiable on (0,1), with f(0)=0 and f(1)=1.
Show that for each positive integer n there exist distinct numbers c1 , ... , cn in (0,1) such that Πk=1n f '(ck ) = 1.
Graphical solution:
According to the mean value theorem, there exists a number c ∈ (0,1) with f '(c) = 1.
Furthermore, the following is clear if we think of the graph of f:
There must exist disjunct intervals I and J within (0,1) such that if a ∈ I and f '(a) = tan(α), there is b ∈ J with f '(b) = tan(π/2 - α) = 1/f '(a).
(Since a and b both run through an interval, the assertion of the problem is rather weak.)
11756 Let f be a function from [-1,1] to (-∞,∞) with continuous derivatives of all orders up to 2n+2.
Given f(0) = f "(0) = ... = f (2n)(0) = 0, prove
(1/2)((2n+2)!)2(4n+5) (∫-11 f(x) dx)2 ≤ ∫-11 (f (2n+2)(x))2 dx.
Partial solution:
First we restrict ourselves to the case that f is a polynomial of degree at most 2n+2.
Then the coefficients of even powers of x (up to exponent 2n) are 0 and the terms with odd powers of x vanish if we integrate them from -1 to 1.
So we have (2n+2)! (∫-11 f(x) dx) = ∫-11 f (2n+2)(0) x2n+2 dx = (2/(2n+3)) f (2n+2)(0).
Furthermore we have f (2n+2)(x) = f (2n+2)(0), so ∫-11 (f (2n+2)(x))2 dx = 2 (f (2n+2)(0))2.
So ((2n+3)2/2) (2n+2)!2 (∫-11 f(x) dx)2 = ∫-11 (f (2n+2)(x))2 dx. Then the inequality amounts to 4n+5 ≤ (2n+3)2.
11757 Prove that the coefficient of xnyn in the power series of 1/((1-3x)(1-(y+3x-x2))) is 9n.
Partial solution:
We use 1/(1-r) = 1 + r + r2 + ... (with r=3x and with r=y+3x-x2).
Then we find the coefficient of xnyn is equal to
Σ0 ≤ k ≤ n 3k Σ(n-k)/2 ≤ j ≤ n-k ((n+j over j)(j over n-k-j)(-1)n-k-j3j).
For any (small) fixed n we may verify this equals 9n.
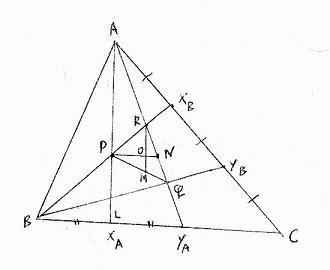
11758 Acute triangle ABC has several ancillary points and properties, shown in the figure.
Segment AXA is perpendicular to BC and segments marked with the same symbol have the same length.
The angle at C is less than the angle at B.
Lines PN and RM are parallel and perpendicular, respectively, to BC.

(a) Prove that |RO|/|OM| = 2.
(b) Show that PQ is not parallel to BC.
(c) Letting D be the intersection of PQ and BC, show that if AD is perpendicular to BXB , then P,R,N and M are on a common circle.
(d) For fixed B and C, describe the set of A such that AD is perpendicular to BXB .
Solution:
Give coordinates in such a way that B(0,0), XA(1,0), YA(2,0), C(a,0) with a > 2, A(1,t) with t > 0.
Then we find XB((2+a)/3,2t/3), YB((1+2a)/3,t/3) and P(1,2t/(2+a)), R((4+2a)/(4+a),4t/(4+a)), N((2+2a)/(2+a),2t/(2+a)), Q((1+2a)/(1+a),t/(1+a)),
M((4+2a)/(4+a),t(8+a)/((2+a)(4+a))) and D(3,0).
(a) Since R,O,M have the same x-coordinate, the distances are differences of y-coordinates and we quickly check |RO|/|OM| = 2.
(b) Since P and Q have distinct y-coordinates, PQ is not parallel to BC.
(c)(d) AD is perpendicular to BXB iff a = t2 - 2.
Then we have P(1,2/t), R(2t2/(2+t2),4t/(2+t2)), M(2t2/(2+t2),(6+t2)/(2t+t3)), N((2t2-2)/t2,2/t).
Now we can check that P,R,N and M are on a common circle by using the cosine rule in triangles PRN and PMN:
it turns out the cosines of the angles at R and M add up to 0, so the angles at R and M add up to 180 degrees.
11761 For each positive integer n, determine the least integer m such that lcm{1,2,...,m} = lcm{n,n+1,...,m}.
Solution:
For all i ∈ {1,2,..,n-1}, the maximal multiplicity of a prime power occurring in the representation of i as a product of prime powers must also occur
in the representation as a product of prime powers of some integer j ∈ {n,n+1,..,m}.
This is true iff m = 2pk, where pk is the greatest prime power smaller than n.
11763 Characterize the twice-differentiable and bounded functions f mapping the set of positive reals into itself and satisfying
x g"(x) + (1 + x g'(x))g'(x) ≥ 0 for all (positive) x, where g = log(f).
Graphical characterization:
The inequality can be reduced to h' + h/x ≥ 0, where h = f '.
So let α be the angle which the line through (0,0) and (x,h(x)) makes with the positive x-axis, and β the angle which the tangent
in (x,h(x)) to the graph of h(x) (for x > 0) makes with the positive x-axis.
Then the inequality is equivalent to tan(α) + tan(β) ≥ 0.
We could also give an economical characterization:
If x is input and h(x) the corresponding profit, marginal profit is never less than average loss.
11771 Let n!! = Πi=0[(n-1)/2](n-2i). Find limn → ∞ ((2n-1)!!)1/n*(tan(π(n+1)!1/(n+1)/(4(n!)1/n)) - 1).
Solution:
I ran a pascal program which yields a slowly ascending sequence of outcomes for n=1 through n=150 with last term 1.14.. .
Using the formula of Stirling, and that (2n-1)!!=(2n-1)(2n-3)..5.3.1 is between (n-1)!2n-1 and n!2n, we find that the limit must be equal to
limn → ∞ (2n/e)*(tan((π/4)(1+1/n)) - 1).
Substituting t=1/n and using the theorem of l'Hôpital, we find the limit is π/e = 1.159..
11774 Let ω be the circumscribed circle of triangle ABC.
The A-mixtilinear incircle of ABC and ω is the circle that is internally tangent to ω, AB and AC, and similarly for B and C.
Let A', PB and PC be the points on ω, AB, and AC, respectively, at which the A-mixtilinear incircle touches.
Define B' and C' in the same manner in which A' was defined. (See figure.)
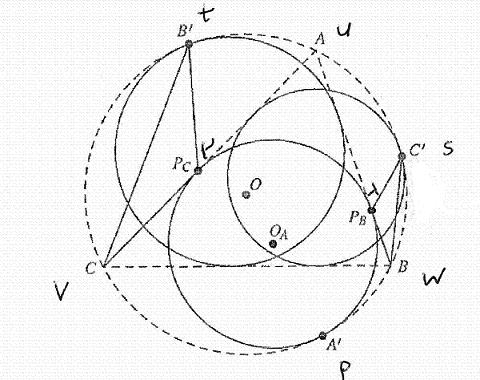
Prove that the triangles C'PBB and CPCB' are similar.
Partial solution:
Give coordinates such that ω: x2 + y2 = 1,
A: (cos(u),sin(u)), B: (cos(w),sin(w)), C: (cos(v),sin(v)),
(see figure) A': (cos(p),sin(p)), B': (cos(t),sin(t)), C': (cos(s),sin(s)),
(see figure) OA: (r cos(p), r sin(p)),
(see figure) PB: (cos(u),sin(u)) + λ((cos(w),sin(w)) - (cos(u),sin(u))), PC: (cos(u),sin(u)) + μ((cos(v),sin(v)) - (cos(u),sin(u))).
We are going to express p,t,s,λ and μ in u,v,w.
Thereafter we can calculate the angles of triangles C'PBB and CPCB', with the cosine rule or simply as angles at the circumference of a circle.
To calculate p,t,s,λ and μ, we use four conditions:
1) OAA' = OAPB, 2) OAA' = OAPC, 3) OAPB is perpendicular to AB,
4) OAPC is perpendicular to AC.
We find r = λ(1-λ)(1-cos(w-u))/(1-λcos(w-p)-(1-λ)cos(p-u)) = μ(1-μ)(1-cos(v-u))/(1-μcos(p-v)-(1-μ)cos(p-u)) =
(2λ-1)(1-cos(w-u))/(cos(w-p)-cos(p-u)) = (2μ-1)(1-cos(v-u))/(cos(p-v)-cos(p-u)).
Hence with λ2/(2λ-1) = (1-cos(p-u))/(cos(w-p)-cos(p-u)) = A and μ2/(2μ-1) = (1-cos(p-u))/(cos(p-v)-cos(p-u)) = B, we find
λ = A - √(A2-A) = 2sin((p-u)/2)(sin(p-u)/2)-sin((w-p)/2))/(cos(w-p)-cos(p-u)) = (sin((p-u)/4) cos((p-u)/4)/((sin((w-u)/4)(cos(2p-u-w)/4)) and
μ = B - √(B2-B) = 2sin((p-u)/2)(sin(p-u)/2)-sin((p-v)/2))/(cos(p-v)-cos(p-u)) = (sin((p-u)/4) cos((p-u)/4)/((sin((v-u)/4)(cos(2p-u-v)/4)) and
and λ/μ = sin((v-u)/2)/sin((w-u)/2) and sin((v-u)/4)/cos((w-u)/4) = sin((2p-u-v)/4)/cos((2p-u-w)/4).
Using goniometric formulas we find sin(p) = 2X/(1+X2) and cos(p) = (1-X2)/(1+X2) with X = tan(p/2) =
(sin((v-u)/4)cos((u+w)/4 + sin((u+v)/4)cos((w-u)/4))/(cos((u+v)/4)cos((w-u)/4 - sin((v-u)/4)sin((u+w)/4)).
Furthermore, we find from the coordinates of A' those of C' by substituting for u,v,w (simultaneously) v,w,u (respectively) and those of B'
by substituting for u,v,w (simultaneously) w,u,v (respectively).
So now we have the coordinates of the vertices of the triangles, and could in principle finish the job, but that would require another day of calculation.
I think this problem can be more easily solved by applying the theory of inversion, but I don't know enough of this theory.
In the picture it seems the lines BB', CC' and PBPC are concurrent, so maybe the triangles are mapped to each other by a reflexion in the point of intersection.
11782 A signed binary representation of an integer m is a finite list a0 , a1 , ... of elements of {-1,0,1} such that Σ ai 2i = m.
A signed binary representation is sparse if no two consecutive entries in the list are nonzero.
(a) Prove that every integer has a unique sparse representation.
(b) Prove that for all integer m, every non-sparse signed binary representation of m has at least as many nonzero terms as the sparse representation.
Solution:
(a) First we prove for every (positive) integer the existence of a sparse representation.
This can be done with induction:
First, we make a list of sparse representations for m with 1 ≤ m ≤ 2k, for instance for k=1 we have the list (1) (0,1).
Next, we see we can derive from it a list of sparse representations for m equal to 2k+1+x with -2k-1 ≤ x ≤ 2k-1
and hence a list of sparse representations for m with 1 ≤ m ≤ 2k+1.
As for the uniqueness: suppose some m would have two distinct sparse representations Σ ai 2i = Σ bi 2i.
Now first cancel ai and bi (same i) if they are equal, next move all remaining negative terms to the other side of the equality sign, and use 2*2j = 2j+1.
Since the representations were sparse and distinct, we would get two distinct (unsigned) binary representations of some nonzero positive integer.
(b) Suppose there would be a non-sparse signed binary representation Σ bi 2i with less nonzero terms
than the sparse signed binary representation Σ ai 2i of the same nonzero number.
We may also assume there are not more negative terms at the left hand side of Σ ai 2i = Σ bi 2i (or else multiply by -1).
Now first cancel ai and bi (same i) if they are equal.
Next move all remaining negative terms to the other side of the equality sign, and use 2*2j = 2j+1 where possible.
(At the right hand side it may then be necessary to repeat this last step, but not at the left hand side, so the number of nonzero terms stays less at the right hand side.)
Then again we would at last find two distinct (unsigned) binary representations of some nonzero positive integer.
11783 Given a tetrahedron, let r denote the radius of its inscribed sphere. For 1 ≤ k ≤ 4, let hk denote the distance from the k-th vertex to the plane of the opposite face.
Prove that Σ1 ≤ k ≤ 4 (hk-r)/(hk+r) ≥ 12/5.
Partial solution:
Of course, by scaling, we may assume r=1. If the tetrahedron is regular we can give
coordinates so that A(0,0,3), B(-√2,-√6,-1), C(-√2,√6,-1), D(2√2,0,-1). Then we find hk=4 for all k with 1 ≤ k ≤ 4 and the sum is 12/5.
It is plausible that the minimum of the sum occurs for regular tetrahedra, but we still have to prove it.
We may start with the four faces at distance 1 from (0,0,0) and equations
sin(θ)cos(α)X + sin(θ)sin(α)Y + cos(θ)Z = 1, sin(θ)cos(β)X + sin(θ)sin(β)Y + cos(θ)Z = 1,
sin(θ)cos(γ)X + sin(θ)sin(γ)Y + cos(θ)Z = 1, sin(σ)cos(τ)X + sin(σ)sin(τ)Y + cos(σ)Z = 1.
Then we still have to calculate the coordinates of the vertices and the distances hk and the minimum of the sum.
It may be easier to prove that the sum is a local minimum for a regular tetrahedron.
Indeed, let's start with a regular tetrahedron whose inscribed sphere has radius r=1 and whose distances from a vertex to the opposite face are h1 = h2 = h3 =
h4 = h (= 4).
If we stretch or press some side(s) of this tetrahedron while keeping the same inscribed sphere, the sum changes with
approximately (2/(h+1)2)(dh1 + dh2 + dh3 + dh4), where the last factor between brackets seems to be always positive.
11784 Let ABC be an equilateral triangle with center O and circumradius r. Given R > r, let ρ be a circle about O with radius R. All points named P are on ρ.
(a) Prove that |PA|2 + |PB|2 + |PC|2 = 3(R2 + r2).
(b) Prove that minP ∈ ρ |PA|*|PB|*|PC| = R3 - r3, and maxP ∈ ρ |PA|*|PB|*|PC| = R3 + r3.
(c) Prove that the area of a triangle with sides of length |PA|,|PB|,|PC| is (√(3)/4)*(R2 - r2).
(d) Prove that if H,K,L are the respective projections of P onto AB, AC, and BC, then the area of triangle HKL is (3√(3)/16)(R2 - r2).
(e) With the same notation, prove that |HK|2 + |KL|2 + |HL|2 = (9/4)(R2 + r2).
Solution:
Give coordinates O(0,0), A(-r√3/2,-r/2), B(r√3/2,-r/2), C(0,r), P(R cos(φ),R sin(φ)).
(a) We find |PA|2 = R2 + r2 + 2rR sin(φ+π/3), |PB|2 = R2 + r2 + 2rR sin(φ-π/3), |PC|2 = R2 + r2 -2rR sin(φ).
(b) The minimum is found for P nearest to a vertex, for example φ = π/2, the maximum for P at equal distance from two vertices, for example φ = 3π/2.
(c) The easiest way to check this is perhaps using Heron's formula for the area of a triangle with sides of length a,b,c: (√((a2 + b2 + c2)2 - 2(a4 + b4 + c4)))/4.
(d)+(e): We find
H(R cos(φ),-r/2),
K((R/4)cos(φ) + (R√3/4)sin(φ) - r√3/4, (R√3/4)cos(φ) + (3R/4)sin(φ) + r/4),
L((R/4)cos(φ) - (R√3/4)sin(φ) + r√3/4, (-R√3/4)cos(φ) + (3R/4)sin(φ) + r/4).
Hence |HK|2 = (3/4)(R2 + r2) + (3rR√3/4)cos(φ) +(3rR/4)sin(φ), |HL|2 = (3/4)(R2 + r2) - (3rR√3/4)cos(φ) +(3rR/4)sin(φ), |KL|2 = (3/4)(R2 + r2) -(3rR/2)sin(φ).
So we find (e) at once, and for (d) we can again use Heron's formula.
11786 Let x1 , x2 , ... be a sequence of positive numbers such that lim n → ∞ xn = 0 and
lim n → ∞ log(xn )/(x1 + ... + xn ) is a negative number.
Prove that lim n → ∞ log(xn )/log(n) = -1.
First observation:
If xn = 1/np with p > 0, it's well known the conditions are satisfied iff p=1. And in this case p=1 the conclusion is valid too.
11788 Let n be a positive integer, and suppose that 0 < yi ≤ xi < 1 for 1 ≤ i ≤ n.
Prove that (log x1 + ... + log xn)/(log y1 + ... + log yn) ≤ √((1-x1)/(1-y1) + ... + (1-xn)/(1-yn)).
First try:
If n=1 and x = x1 = 1-u and y = y1 = 1-v, then we have to prove log(1-u)/log(1-v) ≤ √(u/v) for 0 < u ≤ v < 1.
Using the power series for log, we see this amounts to proving ((u + u2/2 + u3/3 + ...)/(v + v2/2 + v3/3 + ...))2 ≤ u/v for 0 < u ≤ v < 1.
But this is straightforward, so then we are finished with the case n=1.
In general, it's sufficient to prove (Σi=1n Σk=1∞ uik/k)2/(n u1...un) ≤ (Σi=1n Σk=1∞ vik/k)2/(v1...vn) if 0 < ui ≤ vi < 1 for 1 ≤ i ≤ n.
11789 Let a and k be positive integers. Prove that for every positive integer d there exists a positive integer n such that d divides k*an + n.
First exploration:
I've checked the claim for all k,a,d that don't exceed 100, with the help of the following pascal program:
program modulo;
var n,k,a,d,p:integer; klaar:boolean;
begin
for k:=1 to 100 do for a:=1 to 100 do for d:=1 to 100 do
begin
n:=0; p:=1; klaar:=false;
repeat
if (((k*p+n) mod d) = 0) then
begin klaar:=true; writeln(k:6,a:6,d:6,n:6) end;
if not klaar then begin n:=n+1; p:=(p*a mod d) end
until (klaar or (n>10000));
if not klaar then begin writeln(k:6,a:6,d:6,'faalt'); readln end
end; readln
end.
11790 Given a triangle with semiperimeter s, inradius r, and medians of length ma , mb , and mc , prove that ma + mb + mc ≤ 2s - 3(2√3-3)r.
Solution (numerical):
If we denote the side lengths with a,b,c and the angles with α, β, γ, we have by definition 2s = a+b+c and by the sine rule a/sin(α) = b/sin(β) = c/sin(γ) ( = h).
Furthermore, in the literature we find formulas 2ma = √(2b2 + 2c2 - a2), etc, and 2r = √((b+c-a)(a+c-b)(a+b-c)/(a+b+c)).
The inequality then amounts to
√(sin(α) + sin(β) + sin(γ))*(√(2sin2(β) + 2sin2(γ) - sin2(α)) +
√(2sin2(α) + 2sin2(γ) - sin2(β)) + √(2sin2(α) + 2sin2(β) - sin2(γ))) ≤
2(sin(α) + sin(β) + sin(γ))*√(sin(α) + sin(β) + sin(γ)) - 3(2√3-3)√((sin(β) + sin(γ) - sin(α))(sin(α) + sin(γ) - sin(β))(sin(α) + sin(β) - sin(γ))).
We can check with mathematica that this inequality holds for all positive α, β, γ with α + β + γ = π.
There is equality iff α = β = γ = π/3.
11792 Show that every infinite-dimensional Banach space V contains a closed subspace of infinite dimension and infinite codimension.
First guess:
Let e1, e2, e3, ... be a basis of V, consisting of vectors whose norm ||ei|| is equal to 1.
Then I think {x ∈ V / ||x - e1|| ≤ ||x - e2||} could be such a subspace, but I don't know much about Banach spaces.
11794 Find every twice differentiable function f on the real numbers such that for all nonzero x and y holds x f(f(y)/x) = y f(f(x)/y).
Partial solution:
If we try f(t) = a + bt + ct2, dividing by x-y and using a polynomial is zero iff the coefficients are all zero, we find c=0 and a = b2.
Likewise, if we try f(t) = Σk=0n aktk for some natural number n, looking at the coefficient for the term with the highest exponent of x, we find an=0 unless n=1.
So the only polynomial solutions are f(t) = b2 + bt.