PROJECTIVE GEOMETRY COURSE
Chapter 1: INTRODUCTION
§ 1: Central projection
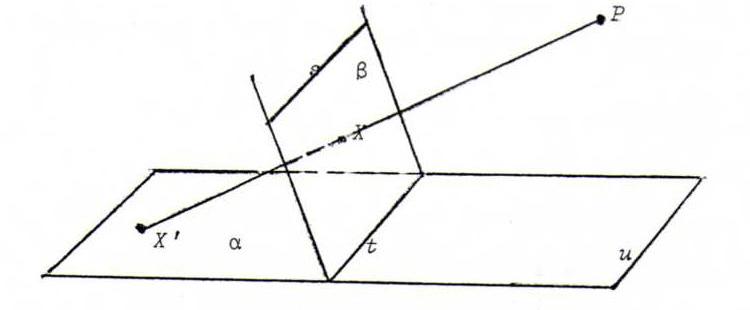
Consider two non-parallel planes α and β and a point P that is not in any of both planes.
Let s be intersecting line of β and the plane through P parallel to α.
Let t be the intersecting line of α and β.
Let u be the intersecting line of α and the plane through P parallel to β.
For each point X in β that is not lying in s, let X' be the point of intersection of α and the line connecting P and X.

The mapping X→X' is a bijection from β/s onto α/u, named central projection. We find:
i) If the points A, B, C in β/s are collinear (on l), then so are the image points A', B',
C' (on l').
ii) If the lines a, b and c in β concur in a point L of β/s, then the image lines a',
b' and c' concur in L'.
iii) If l and m are parallel lines in β that intersect s in distinct points, then l'
and m' intersect in a point of u.
iv) If l and m are lines in β, parallel to s but not identical to s, or intersecting in a point of s,
then l' and m' are parallel.
v) Let d(A,B) be the distance between A and B. Suppose that A, B and C are collinear in β/s.
In general we have d(A,B) ≠ d(A',B') and d(A,B)/d(B,C) ≠ d(A',B')/d(B',C').
vi) Let ∠(l,m) be the smallest angle between l and m. Let A, B and C be non-collinear points in β/s.
In general, we find ∠(AB,BC) ≠ ∠(A'B',B'C').
vii) The image of a circle c in β is a conic section in α: an ellipse if c and s don't intersect, a parabola if c
touches s, and an hyperbola if c and s intersect in two points.
We provisionally define projective geometry as the study of those geometrical concepts that are invariant under central projection.
We have, among others, the following projective concepts:
a) points, lines, incidence of points and lines (a point A is incident with a line l if A lies on l);
collinearity and concurrence, complete triangles and complete quadrangles;
b) separation and cross ratio
(let A, B, C, D be four points on a line l, then the pairs {A,B} and
{C,D} separate if one of the points C and D lies between A and B, and the other doesn't;
the cross ratio
(A,B;C,D) is the number (d(A,C)/d(A,D)):(d(B,C)/d(B,D)), provided with a
minus sign if {A,B} and {C,D} separate), see section 9.
Concepts like distance and ratio of distances, measure of angles, ellipse, parabola and hyperbola, parallel, are not projective concepts (but the concepts conic and touching are).
Problems:
O1 Verify all assertions above.
O2 When we use parallel projection instead of central projection, we replace the bundle of lines through P by a bundle of parallel lines that intersect α and β.
A geometrical concept that is invariant under parallel projection is called an affine concept. Which of the concepts mentioned above are zijn affine?
O3 Let l be a line in β that intersects s in S, and l' its image line in α. Let c be a circle that touches l'. Give the instructions for a continuous mapping from l onto c.
O4 Suppose that the circle c in β intersects the line s in A and B, so that the image curve is a hyperbola.
Which lines in β are corresponding to the asymptotes of this hyperbola?
Explain by reference to the situation in β that the lines in α with asymptotical direction intersect the hyperbola in at most one point.