PROJECTIVE GEOMETRY COURSE
§ 17: Classification of the central collineations
Proposition : A central collineation is uniquely determined by its centre C, axis a, and one pair {X,X ' } of point and image point, provided
C, X, X ' are collinear and X ≠ X ' .
Proof: Now we can construct for Y in P2 the image point Y ' (see O14).
Definition : We call the central collineation an elation if the centre C lies on the axis a, and otherwise we call it a homology.
In the second case we call it a harmonic homology if there exists a point X such that X and X ' lie harmonically with respect to C and
SX , where SX = CX.a .
As to this, see also the following proposition and its proof.
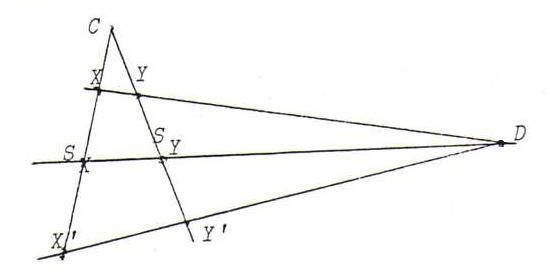
Proposition : A harmonic homology is uniquely determined by its centre and its axis.
Proof: Let X be a point as in the definition above. Let Y be a point not on CX and not on a. According to O14 we have the following picture:

So {Y,Y ' } and {C,SY} are also pairs that separate harmonically.
Now by reasoning with Y instead of X we see that the points on CX are, with their image points, harmonically situated with respect to C and SX.
Proposition : An elation is uniquely determined by its axis a and one pair {X,X ' } with X, ≠ X ' .
Proof: Then the centre C is the intersection point of a and XX ' (see the proof of the main theorem about collineations).
For the rest, see the first proposition of this section.
Proposition : Let φ be an involutory projective transformation. Then φ is a harmonic homology.
Proof: φ is involutory, so if φ(X) = X ' , then φ(X ' ) = X.
Now consider the complete quadrangle AA ' BB ' .
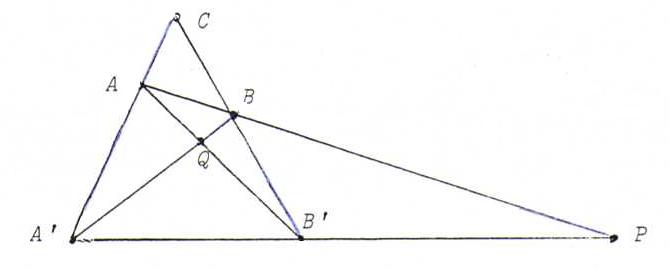
The lines AA ' and BB ' are invariant, so the intersection point C := AA ' .BB ' is also invariant.
Since φ interchanges the lines AB and A ' B ' , P := AB. A ' B ' is invariant.
Likewise, Q := A ' B. AB ' is invariant. So the line PQ is invariant, too.
Since AA ' and BB ' are also invariant, AA ' .PQ and BB ' .PQ are invariant, too.
So the line PQ contains already at least four fixed points, so it is pointwise invariant (propositions of §10).
So φ is a homology with centre C and axis PQ.
Now {A,A ' } and {C,S} both separate harmonically with S := PQ. AA ' (see §12), so φ is a harmonic homology.
Note: φ induces a hyperbolice involution on every line through C.
Note: the inverse proposition also holds.
Problem 65: Suppose we have a central collineation with centre C, axis a, line x (not through C) and image line x ' .
Prove that x. x ' lies on a.
Let Y be a point unequal to C and not on a. Construct Y ' .
Problem 66: Construct the matrix of the harmonic homology φ with centre λ(0,0,1) and axis x3=0.
Problem 67: Give a parameter representation for the matrices of elations with axis λ(1,1,1) and centre λ(0,1,-1).
Problem 68: Prove that the following matrix belongs to a central collineation, and determine the centre and the axis: λ((7,-99,-33),(2,-22,-6),(-1,9,-1)).
Problem 69: Consider the projective transformation φ with matrix λ((-√2,0,√2),(0,2,0),(√2,0,√2)).
Prove that φ is a harmonic homology and determine the projective coordinates of the centre and the axis.
Problem 70: Prove that the matrix of a central collineation φ with axis x3 = 0 has the following form:
λ((α,0,β),(0,α,γ),(0,0,1)) with α≠0.
Prove that φ is an elation if α=1 and (β,γ)≠(0,0).
Determine in that case the centre of the elation.