PROJECTIVE GEOMETRY COURSE
§ 2: Models of a projective geometry
Definition: a model of a (plane) projective geometry is a triple that consists of:
a non-empty set P whose elements we call points;
a non-empty set L whose elements we call lines;
an incidence relation to which every un-ordered pair of point and line either belongs or does not belong;
whilst the following axioms are satisfied:
A1 each line is incident with at least three points;
A2 each point is incident with at least three lines;
A3 with each pair of points there is exactly one line that is incident with both points;
A4 with each pair of lines there is exactly one point that is incident with both lines.
We call the axioms A1 and A2 dual to each other; likewise the axioms A3 and A4 are dual.
As a consequence of the fact that each axiom has a dual axiom, we find that, with each proposition we deduce from the axioms, a dual propsition can likewise be deduced.
This is the principle of duality.
By interchanging the roles of P and L in the definition above, we get the dual model.
The most important model of a projective geometry is the real projective plane.
We are given space with in it a fixed point O.
P is the set of straight lines through O, L is the set of planes through O.
A point p belonging to the set P is incident with the line l belonging to the set L if the straight line p
lies in the plane l.
Check that the axioms are satisfied.
Now consider ℜ3 with in it the plane x3=1.
Let P' be the set of points in that plane, and L' the set of lines in that plane, with the common incidence relation.
This is not a model of a projective geometry, because A4 is not satisfied. To repair this, we consider the so-called points at infinity and the line at infinity.
Definition : A point at infinity is an equivalence class of parallel lines. The line at infinity is the set of points at infinity.
O5 Let P" := P'∪{points at infinity}. Let L" := L'∪{line at infinity}.
How must we define an incidence relation so that the triple of P", L" and this incidence relation is a model of a projective
geometry?
First define a bijection A:P→P" and a bijection B:L→L", and make p from P incident
with l from L if and only if Ap is incident is with Bl (we call the models isomorphic).
O6 Let B be a sphere with centre O as above.
Let P''' be the set of the pairs of antipodal points on B, and L''' the set of great circles on B, with the
common incidence relation.
Show that this model is isomorphic with the real projective plane.
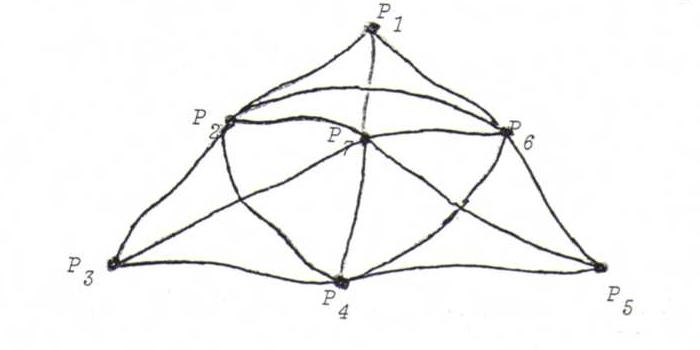
O7 A model of the seven points geometry:
This consists of seven beads P1, P2, ... , P7 (the points) and seven threads
L1, L2, ... , L7 (the lines), with incidence as in the picture beneath
(points and lines get arbitrary running numbers).

Make an incidence matrix, and check the axioms. Why do we call this seven points geometry selfdual?
Prove that each model of a projective geometry contains at least seven points and at least seven lines.