A quadratic surface is the set of points in ℜ3 that satisfy an equation of the form
a1 1x12 + a2 2x22 + a3 3x32 + 2 a1 2x1x2 + 2 a1 3x1x3 + 2 a2 3x2x3 = 0 (for given real numbers ai j).
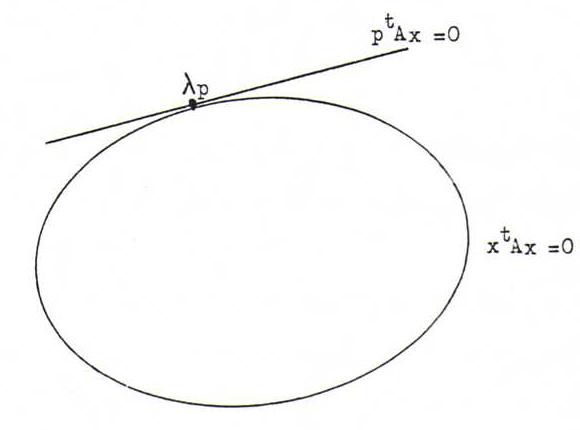
Such a quadratic surface exists of straight lines through O, and hence we call it a cone with top O. In this section we will see that the intersection of the quadratic surface with the plane x3 = 1 is a parabola, a hyperbola or an ellipse.
Speaking in projective terms, each straight line through O is a point, and the quadratic surface a conic (parabolas, ellipses and hyperbolas are (together with their degenerated versions) exactly the possible intersection figures of of a common right circular cone and a plane).
The inhomogeneous equation is a1 1x12 + a2 2x22 + a3 3 + 2 a1 2x1x2 + 2 a1 3x1 + 2 a2 3x2 = 0, or (in matrix notation)
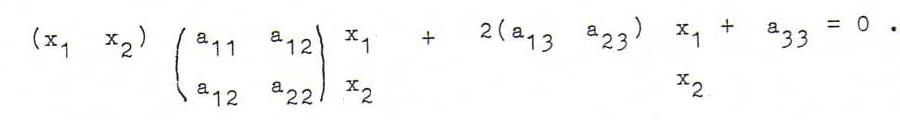
Short notation of this matrix equation: xt A x + 2 at x + a3 3 = 0.
The symmetric matrix A has two real eigenvalues λ1 and λ2 (that possibly coincide), and there is in ℜ2 an orthonormal base consisting of eigenvectors of this matrix: say r1, r2, where Ar1 = λ1r1, Ar2 = λ2r2.
Use coordinates y1 and y2 with respect to this new base, so x = y1r1 + y2r2, or, in an other notation, x = Ry where r1 stands in the first column of R and r2 in the second column. Then the matrix R is orthogonal, which means Rt = R-1. Now check by calculation that RtAR is the diagonal matrix with eigenvalues λ1 and λ2 on the diagonal.
So in the new coordinates the matrix equation becomes ytRt A Ry + 2 at Ry + a3 3 = 0, or
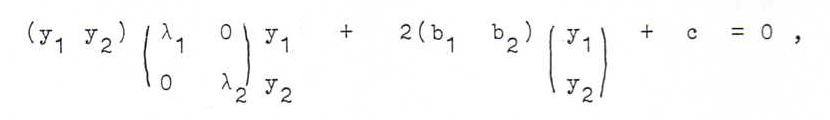
short λ1y12 + λ2y22 + 2 b1y1 + 2 b2y2 + c = 0.
If λ1λ2 = 0 we get the equation of a parabola.
Else, if λ1λ2 is positive, we have the equation of an ellipse, and if λ1λ2 is negative the equation of a hyperbola.