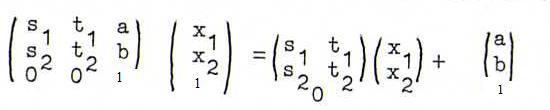
PROJECTIVE GEOMETRY COURSE
§ 6: PM as a base for geometries with a finer structure
We start from the real projective plane of the straight lines and planes through O. A projective transformation is a bijection from this projective plane onto itself that preserves the
incidence of points and lines and the cross ratio.
Let GP be the group of projective transformations, and LR3 the group of regular linear transformations of ℜ3. For A ∈ LR3, let
φA be the projective transformation induced by A (see O61). Then A→φA is a surjective group homomorphism from LR3
to GP with kernel {λI / λ≠0}. So GP ≅ LR3/{λI / λ≠0}.
Let M3 be the group of regular 3 x 3 matrices with real coefficients, so that M3 ≅ LR3, and let E3 be the 3 x 3 matrix
with 1 on the diagonal and 0 off the diagonal. Then we also have GP ≅ M3/{λE3 / λ≠0}. So, every projective transformation has a matrix
that is unique up to a multiplication with a scalar λ.
Now take an arbitrary line out of P2 and call it the line at infinity. We ourselves take the line l∞ corresponding with {x3=0}.
The projective transformations that map l∞ onto itself form a subgroup of GP, the affine group GA, and are called affine transformations.
In this § we further identify each affine transformation with a regular linear transformation of ℜ3 that maps {x3=0} to itself and (0,0,1) to
(a,b,1). The matrix then has as its last row 0 0 1 and maps the points of {x3=1} according to
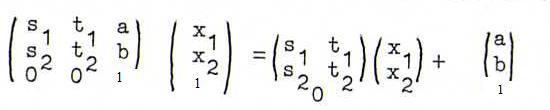
; hence, such an affine transformation is the product of: first an orthogonal projection onto {x3=0}, then a linear transformation in {x3=0}, and finally a translation with translation vector (a,b,1).
A similarity transformation is an affine transformation that works in {x3=0} as a product of a rotation or reflection and a positive scalar (the similarity factor). So the matrix of a similarity transformation has the form
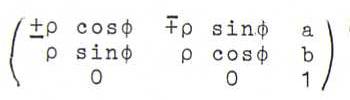
(with similarity factor ρ).
The similarity transformations form the similarity group GS.
Finally we define a congruence transformation as a similarity transformation with similarity factor 1. The congruence transformations form the congruence group GC.
Thus we find GC⊂GS⊂GA⊂GP.
For X∈{P, A, S, C} we define a X-concept as a concept that is invariant under the
transformations of GX.
So {P-concepts}⊂{A-concepts}⊂{S-concepts}⊂{C-concepts}.
For example, points, lines and incidence are P-concepts, parallel is an A-concept, angle a S-concept, and distance a C-concept.
We define the X-geometry as the geometry of the X-concepts. The C-geometry is the good old euclidian geometry.
O22 Define the concept "parallel" in A-geometry, and show this is not a P-concept.
O23 Prove that "angle" is a S-concept, and "distance" a C-concept.
O24 Give for each of the following concepts the letters X so that that concept is a X-concept: quadrilateral, parallellogram, rhomb, square.
O25 We call two figures X-equal if there is an element of GX that maps one of them into the other. Are any two conics A-equal?
O26 Suppose we have three proper points A, B and C on a line l, and the point at infinity L∞ on l.
Define the following A-concepts using cross ratio (We count ∞/∞=1; a/∞=0, ∞/a=∞ for a≠∞,0 (resp.); XY=-YX; etc.)
i) "X lies between A and B on l ";
ii) "AB is three times as great as BC ";
iii) "B is the centre of AC ".