PROJECTIVE GEOMETRY COURSE
§ 7: PM as a base for non-euclidean geometries
Euclid included in his set of axioms the socalled fifth postulate: "Given a point P that's not lying on a (straight) line l, there's exactly one line through P that doesn't
intersect l".
In an unrefined projective geometry this postulate isn't always satisfied. However, we only call a geometry non-euclidean if the concepts perpendicular and distance are defined in it in a sensible
way, whilst the fifth postulate isn't satisfied.
Example 1: the elliptic plane. Start with the sphere model of the real projective plane (see O6). We call the pairs of antipodal points elliptic points, and the great circles
on the sphere with radius 1 elliptic lines.
For elliptic points P and Q, define elliptic distance d(P,Q) as the length of the smallest circular arc between a representative of P and a
representative of Q on the great circle containing both pair of points. In a formula:
d(P,Q) = arccos( (p1q1+p2q2+p3q3)/(√(p12+p22+p32)
√(q12+q22+q32))).
So we have d(P,Q) ∈ [0,π/2].
Furthermore, we define for elliptic lines l and m: l is perpendicular to m if and only if the plane of l in ℜ3 is perpendicular to the plane of m in ℜ3, so if l1m1+l2m2+l3m3=0. See O27.
Example 2: the hyperbolic plane. Consider in ℜ3 the cone k := {x12+x22 = x32} and its
interior {x12+x22 < x32}.
We define:
i) A hyperbolic point is a straight line though the origin which, except for its intersecting point with k (the origin), lies entirely within k.
ii) If a plane through O intersects the cone in two straight lines, we call the part of the plane within k a hyperbolic line.
If we consider the intersection of the hyperbolic points and lines with the plane x3=1, we get the circle model of the hyperbolic plane:

Now define for hyperbolic points P:λ(p1,p2,p3) and Q:λ(q1,q2,q3) the hyperbolic
distance by
d(P,Q) = arccosh( |p3q3-p1q1-p2q2|/(√(p32-p2-p22)
√(q32-q12-q22))).
See O29.
Define for hyperbolic lines l and m hyperbolic orthogonality as follows: l is perpendicular to m if and only if l3m3-l1m1-l2m2=0.
O27 A plane through O in ℜ3 together with its normal define an elliptic line l1 and an elliptic point P1 that are
polar conjugates (P1 is the pole of l1 and l1 is the polar line of P1). Check the following:
a) Each elliptic line through P1 is perpendicular to l1;
b) l1 = {P/d(P,P1)=π/2};
c) P is on the polar line of Q ⇔ Q is on the polar line of P;
d) When P runs through a line l1, then the polar line of P runs through the set of elliptic lines through P1.
O28 Given an hyperbolic point P that doesn't lie on a hyperbolic line l, check that there are an infinite number of hyperbolic lines through P that don't intersect l.
O29 Prove that hyperbolic distance is welldefined and symmetrical, and that we have: d(P,Q) ≥ 0, and [d(P,Q)=0 ⇔ P=Q].
O30 Show that the hyperbolic plane is infinitely large if we measure it in the hyperbolic way.
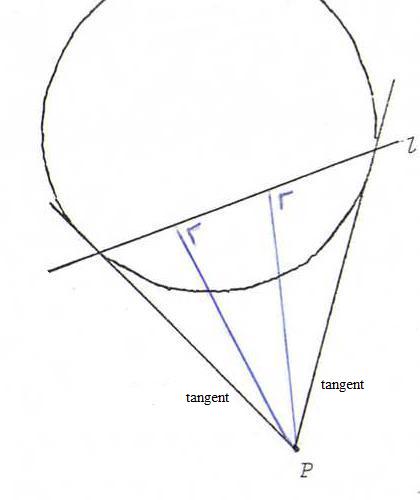
O31 Consider the circle model of the hyperbolic plane.
Check by calculation that in the following picture, where l is the polar line of P, each line "through P"
is hyperbolically perpendicular to l. (Hint: first show that the equation of l in homogeneous coordinates is
xxP + yyP = zzP.)