Hoofdstuk 4: PROJECTIEVE EIGENSCHAPPEN VAN KEGELSNEDEN

§ 20: Classificatie van kwadrieken

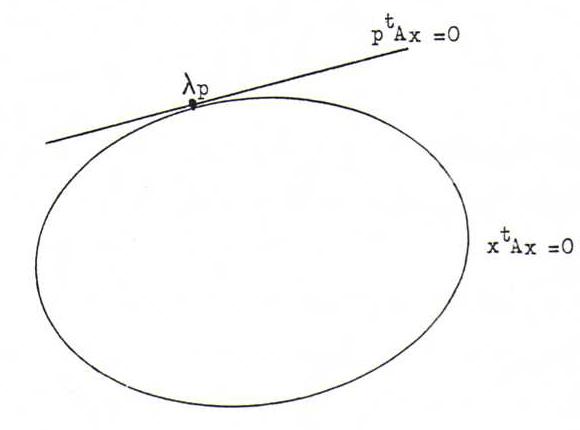
Een kwadriek is de meetkundige plaats in ℜ³ van de punten die voldoen aan een vergelijking van de vorm
a_{1 1}x₁² + a_{2 2}x₂² + a_{3 3}x₃² + 2 a_{1 2}x₁x₂ + 2 a_{1 3}x₁x₃ + 2 a_{2 3}x₂x₃ = 0 (voor gegeven reële getallen a_{i j}).
Zo'n kwadriek bestaat dus uit rechten door O, en heet daarom kegel met top O. In deze paragraaf zullen we zien dat de kwadriek het vlak x₃ = 1 snijdt volgens een parabool, hyperbool of ellips.
Projectief gezien is elke rechte door O een punt, en de kwadriek een kegelsnede (parabolen, ellipsen en hyperbolen zijn (met hun ontaarde versies) precies de mogelijke snijfiguren van een rechte cirkelkegel met een plat vlak).
De inhomogene vergelijking is a_{1 1}x₁² + a_{2 2}x₂² + a_{3 3} + 2 a_{1 2}x₁x₂ + 2 a_{1 3}x₁ + 2 a_{2 3}x₂ = 0, ofwel (in matrixnotatie)

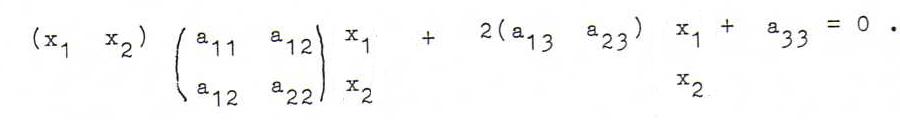
Korte notatie van deze matrixvergelijking: x^t A x + 2 a^t x + a_{3 3} = 0.
De symmetrische matrix A heeft twee (eventueel samenvallend) reële eigenwaarden λ₁ en λ₂, en er is in ℜ² een orthonormale basis bestaande uit eigenvectoren van deze matrix: zeg r₁, r₂, waarbij Ar₁ = λ₁r₁, Ar₂ = λ₂r₂.
Ga over op coördinaten ten opzichte van deze nieuwe basis middels x = y₁r₁ + y₂r₂, of, anders genoteerd, x = Ry waarbij r₁ in de eerste kolom van R staat en r₂ in de tweede. De matrix R is dan orthogonaal, dat wil zeggen R^t = R^-1. Ga nu na dat R^tAR de diagonaalmatrix is met de eigenwaarden λ₁ en λ₂ op de diagonaal.
In de nieuwe coördinaten wordt de matrixvergelijking dus y^tR^t A Ry + 2 a^t Ry + a_{3 3} = 0, ofwel

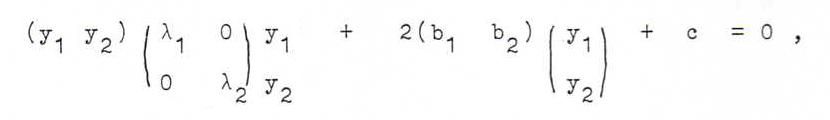
kort λ₁y₁² + λ₂y₂² + 2 b₁y₁ + 2 b₂y₂ + c = 0.
Als λ₁λ₂ = 0 staat er de vergelijking van een parabool.
Anders, als λ₁λ₂ positief is staat er de vergelijking van een ellips, en als λ₁λ₂ negatief is die van een hyperbool.

O79 Voer dit eens uit met x₁² + 2 x₁ x₂ + x₂² + 3 x₁ + 1 = 0, en met 2 x₁² + 2√2 x₁ x₂ + 3 x₂² + x₂ = 0.

We gaan nu de vergelijking opstellen van de raaklijn in een punt van de kegelsnede.
Zij x^tAx = 0 de vergelijking (in homogene coördinaten) van een kegelsnede, en zij λp een punt van de kegelsnede, zodat p^tAp = 0.
Laat λp + μq een willekeurige lijn door λp voorstellen.
Snijden met x^tAx = 0 geeft λ² p^tAp + λμ(p^tAq + q^tAp) + μ² q^tAq = 0, dus ook μ(2λ p^tAq + μ q^tAq) = 0.
Nu is μ = 0 dan en slechts dan een dubbele oplossing van deze vergelijking (en dus λp dubbel snijpunt van de lijn met de kegelsnede) als p^tAq = 0.
Is x = λp + μq, dan p^tAq = 0 ↔ p^tAx = 0, dus p^tAx = 0 is de vergelijking van de raaklijn in λp aan de kegelsnede x^tAx = 0.
Men vindt de vergelijking van de raaklijn in een punt van de kegelsnede dus met de methode van 'eerlijk delen'.

O80 Welke is de vergelijking van de raaklijn in λ(0,-1,1) aan de kegelsnede x₁² + 2 x₂ x₃ + x₂² + 3 x₁ x₃ + x₃² = 0?

uitwerkingen