Gegeven in ℜ3 twee lijnen l en m door 0 , met richtingsvectoren l en m.
Zij A een reguliere lineaire transformatie van ℜ3 met A(l) = m en A(m) = n (n niet in het vlak opgespannen door l en m).
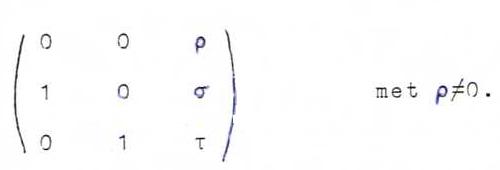
Op basis l, m, n is de matrix van de vorm
CURSUS PROJECTIEVE MEETKUNDE
§ 21: Inleiding vanuit de analytische meetkunde
Gegeven in ℜ3 twee lijnen l en m door 0 , met richtingsvectoren l en m.
Zij A een reguliere lineaire transformatie van ℜ3 met A(l) = m en A(m) = n (n niet in het vlak
opgespannen door l en m).
Op basis l, m, n is de matrix van de vorm

Een willekeurig vlak door l heeft, in coördinaten t.o.v. l, m, n, vergelijking β y' + γ z'= 0 en vectorvoorstelling u(1,0,0) + v(0,-γ,β).
Dit vlak wordt door A afgebeeld op het vlak door m met vectorvoorstelling u(0,1,0) + v(ρβ, σβ, -γ+τβ) en vergelijking
(γ-τβ)x'+ ρβz'= 0.
De meetkundige plaats van de snijlijnen van vlak en beeldvlak vindt men door eliminatie van β en γ. Er komt (zie O81): x'y' + τx'z' = ρ(z')2.
Neemt men nu coördinaten (x,y,z) t.o.v. de natuurlijke basis, dan vindt men via de formule

(ax+by+cz)(dx+ey+fz) + τ(ax+by+cz)(gx+hy+iz) = ρ(gx+hy+iz)2.
Dit is de vergelijking van een willekeurige kegelsnede.
Dit rechtvaardigt de volgende projectieve definitie van een kegelsnede: een kegelsnede is de verzameling der snijpunten x.φ(x), waarbij φ een projectieve transformatie van P2 is en x een lijnenwaaier doorloopt.
Merk op: als n wel in het vlak van l en m ligt, dan vindt men drie punten L, M, N in P2 met φA(L) = M, φA(M) = N, terwijl L, M, N collineair zijn. Volgens de duale van O40 is φA|L dan een perspectiviteit, zodat de kegelsnede ontaardt in twee lijnen (LM en de perspectiviteitsas). Ontaardingen treden ook op als L = M (ga na welke; onderscheid φ = id, φ hyperbolisch, elliptisch of parabolisch).
Stelling: De kegelsnede k: xtAx = 0 is dan en slechts dan ontaard als det(A) = 0.
Bewijs:
1. Stel dat k ontaard is.
Als k één punt is, is de vergelijking van de vorm (px+qy+rz)2 + (ux+vy+wz)2 = 0. Ga na dat dan det(A) = 0.
Anders bestaan er twee verschillende punten P en Q zo dat de lijn PQ geheel op k ligt. Dan is (p+aq)tA(p+aq) = 0 voor alle a, dus ptAp = ptAq =
qtAp = qtAq = 0. Dan liggen de punten λAp en λAq allebei op de lijnen met projectieve coördinaten λp en λq respectievelijk, dus Ap = μAq.
Dan is A(p-μq) = 0 terwijl p ≠ μq, dus det(A)=0.
2. Stel dat det(A)=0.
Dan is Im A een vlak door O of een rechte door O. De vectoren Ap met p op k liggen dan in één vlak, Maar als k niet-ontaard is, is Ap normaal van het vlak door O en de raaklijn in
P aan k. Dus moet k ontaard zijn.
Opmerking : Er bestaan ook lege ('nuldelige') kegelsneden, zoals x2+y2+z2 = 0. Deze laatste heeft A=E3, dus det(A) ≠ 0; we noemen hem niet-ontaard.
O81 Elimineer β en γ uit β y' + γ z' = (γ - τ β) x'+ ρβ z' = 0 (β, γ ≠ 0).
O82 Bewijs, uitgaande van a1 1x12 + a2 2x22 + a3 3x32 + 2 a1 2x1x2 + 2 a1 3x1x3 + 2 a2 3x2x3 = 0, dat door vijf punten in het algemeen precies één kegelsnede gaat (als deze vijf punten vrijgelegen zijn gaat er precies één niet-ontaarde kegelsnede doorheen).