§ 6: PM als grondslag voor meetkunden met een fijnere structuur

We gaan uit van het reële projectieve vlak der rechten en vlakken door O. Een projectieve transformatie is een bijectie van dit projectieve vlak op zichzelf die de incidentie van punten en lijnen bewaart en ook de dubbelverhouding.
Zij GP de groep der projectieve transformaties, en LR³ de groep der reguliere lineaire transformaties van ℜ³. Voor A ∈ LR³ zij φ_A de door A geïnduceerde projectieve transformatie (zie O61). Dan is A→φ_A een surjectief groepshomomorfisme van LR³ naar GP met kern {λI / λ≠0}. Dus GP ≅ LR³/{λI / λ≠0}.
Zij M³ de groep der reguliere 3 bij 3 matrices met reële coëfficiënten, zodat M³ ≅ LR³, en zij E₃ de 3 bij 3 matrix met 1 op de diagonaal en 0 erbuiten. Dan geldt ook GP ≅ M³/{λE₃ / λ≠0}. Iedere projectieve transformatie heeft dus een matrix die tot op een λ-voud na eenduidig bepaald is.

Neem nu een willekeurige lijn uit P² en noem die de oneigenlijke rechte. Wij nemen hiervoor de lijn l_∞ die correspondeert met {x₃=0}.
De projectieve transformaties die l_∞ op zichzelf afbeelden vormen een ondergroep van GP, de affiene groep GA, en heten affiene transformaties.
In deze § identificeren we verder elke affiene transformatie met een reguliere lineaire transformatie van ℜ³ die {x₃=0} in zichzelf overvoert en (0,0,1) in (a,b,1). De matrix heeft dan laatste rij 0 0 1 en werkt op punten van {x₃=1} volgens

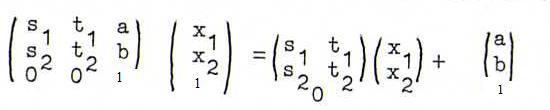
; daarom is zo'n affiene transformatie het product van : eerst een loodrechte projectie op {x₃=0}, dan een lineaire transformatie in {x₃=0}, en tenslotte een translatie over (a,b,1).

Een gelijkvormigheidstransformatie is een affiene transformatie die in {x₃=0} een positief scalair veelvoud (de gelijkvormigheidsfactor) van een draaiing of spiegeling teweegbrengt. De matrix van een gelijkvormigheidstransformatie is dus van de vorm

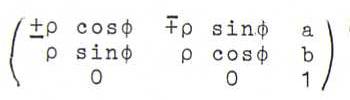
(met gelijkvormigheidsfactor ρ).
De gelijkvormigheidstransformaties vormen de de gelijkvormigheidsgroep GG.

Tenslotte definieert men een congruentietransformatie als een gelijkvormigheidstransformatie met gelijkvormigheidsfactor 1. De congruentietransformaties vormen de congruentiegroep GC.

Zo vinden we GC⊂GG⊂GA⊂GP.
Voor X∈{P, A, G, C} definieert men een X-begrip als een begrip dat invariant is onder de transformaties van GX.
Dus {P-begrippen}⊂{A-begrippen}⊂{G-begrippen}⊂{C-begrippen}.
Zo zijn punten, lijnen en incidentie P-begrippen, is evenwijdigheid een A-begrip, hoek een G-begrip, en afstand een C-begrip.

Men definieert de X-meetkunde als de meetkunde der X-begrippen. De C-meetkunde is de vanouds bekende euclidische meetkunde.

O22 Definieer het begrip evenwijdigheid in de A-meetkunde, en laat zien dat dit geen P-begrip is.

O23 Bewijs dat "hoek" een G-begrip is, en "afstand" een C-begrip.

O24 Geef bij elk der volgende begrippen de letters X zo dat dat begrip een X-begrip is: vierhoek, parallellogram, ruit, vierkant.

O25 Twee figuren heten X-gelijk indien er een element van GX is dat de een in de ander overvoert. Is elk tweetal kegelsneden A-gelijk?

O26 Gegeven drie eigenlijke punten A, B en C op een lijn l, en het oneigenlijk punt L_∞ op l.
Definieer de volgende A-begrippen m.b.v. de dubbelverhouding: (men rekent ∞/∞=1; a/∞=0, ∞/a=∞ voor a≠∞,0 (resp.); XY=-YX; etc.)
i) "X ligt tussen A en B op l ";
ii) "AB is driemaal zo groot als BC ";
iii) "B is het midden van AC ".

uitwerkingen