§ 7: PM als grondslag van niet-euclidische meetkunden

Euclides voegde aan zijn axioma's het zogenaamde vijfde postulaat toe: "Door een punt P, niet op een lijn l, gaat precies één lijn die l niet snijdt".
In een onverfijnde projectieve meetkunde is aan dit postulaat niet per se voldaan. We noemen een meetkunde echter pas niet-euclidisch indien daarin een loodrechtheid en een afstandsbegrip zinvol gedefinieerd zijn, terwijl aan het vijfde postulaat niet voldaan is.

Voorbeeld 1: het elliptische vlak. Ga uit van het bolmodel van het reële projectieve vlak (zie O6). De antipodale puntenparen heten elliptische punten, en de grote cirkels op de eenheidsbol elliptische lijnen.

Definieer voor elliptische punten P en Q de elliptische afstand d(P,Q) := de lengte van de kleinste cirkelboog tussen een representant van P en een representant van Q op de grote cirkel die beide puntenparen bevat. In formule:
d(P,Q) = arccos( (p₁q₁+p₂q₂+p₃q₃)/(√(p₁²+p₂²+p₃²) √(q₁²+q₂²+q₃²))).
Er geldt dus d(P,Q) ∈ [0,π/2].

Definieer voor elliptische lijnen l en m: l staat loodrecht op m precies dan als het vlak van l in ℜ³ loodrecht staat op het vlak van m in ℜ³, dus als l₁m₁+l₂m₂+l₃m₃=0. Zie verder O27.

Voorbeeld 2: het hyperbolische vlak. Beschouw in ℜ³ de kegel k := {x₁²+x₂² = x₃²} en zijn binnengebied {x₁²+x₂² < x₃²}.
We definiëren:
i) een hyperbolisch punt is een rechte door de oorsprong die, op zijn snijpunt met k (de oorsprong) na, geheel binnen k ligt.
ii) Indien een vlak door O de kegel volgens twee beschrijvenden snijdt, dan heet het vlakdeel binnen k een hyperbolische lijn.

Indien men van de hyperbolische punten en lijnen de doorsnijding met x₃=1 neemt, heeft men het cirkelmodel van het hyperbolische vlak:

Definieer nu voor hyperbolische punten P:λ(p₁,p₂,p₃) en Q:λ(q₁,q₂,q₃) de hyperbolische afstand door
d(P,Q) = arccosh( |p₃q₃-p₁q₁-p₂q₂|/(√(p₃²-p²-p₂²) √(q₃²-q₁²-q₂²))).
Zie O29.

Definieer voor hyperbolische lijnen l en m hyperbolische orthogonaliteit als volgt: l staat loodrecht op m precies dan als l₃m₃-l₁m₁-l₂m₂=0.

O27 Een vlak door O in ℜ³ en zijn normaal definiëren een elliptische lijn l₁ en een elliptisch punt P₁ die poolverwant heten (P₁ is pool van l₁ en l₁ is poollijn van P₁). Ga na:
a) Elke elliptische lijn door P₁ staat loodrecht op l₁;
b) l₁ = {P/d(P,P₁)=π/2};
c) P op poollijn van Q ⇔ Q op poollijn van P;
d) Indien P de puntenreeks l₁ doorloopt, dan doorloopt de poollijn van P de elliptische lijnenschaar door P₁.

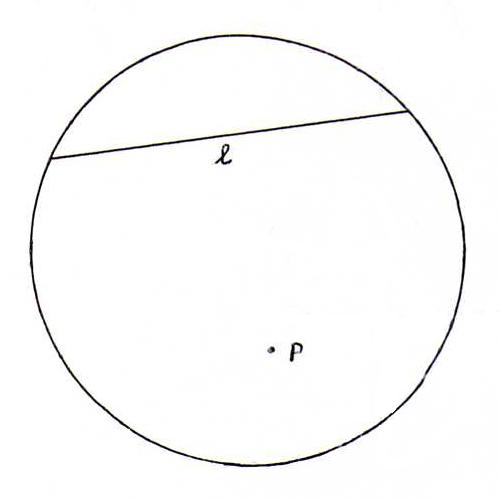
O28 Ga na dat door een hyperbolisch punt P, niet op een hyperbolische lijn l, oneindig veel hyperbolische lijnen gaan die l niet snijden.

O29 Bewijs dat de hyperbolische afstand welgedefinieerd en symmetrisch is, en dat geldt: d(P,Q) ≥ 0, en [d(P,Q)=0 ⇔ P=Q].

O30 Laat zien dat het hyperbolische vlak, hyperbolisch gemeten, oneindig groot is.

O31 Beschouw het cirkelmodel van het hyperbolische vlak.
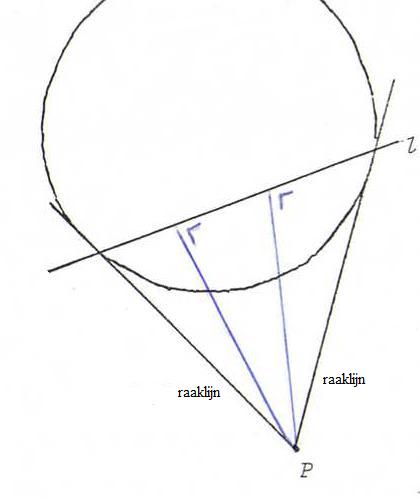
Reken na dat in het volgende plaatje, waarin l de poollijn van P is, elke lijn "door P" hyperbolisch orthogonaal is met l. (Aanwijzing: toon eerst aan dat de vergelijking van l in homogene coördinaten luidt xx_P + yy_P = zz_P.)

uitwerkingen